题目内容
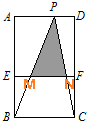
 如图,ABCD是个长方形,BCFE是个正方形,AB为10厘米,BC为4厘米,P为AD边上任意一点.图中阴影部分的面积是
如图,ABCD是个长方形,BCFE是个正方形,AB为10厘米,BC为4厘米,P为AD边上任意一点.图中阴影部分的面积是7.2
7.2
平方厘米.分析:根据题干可得:AD∥EF∥BC,所以△PMN与△PBC相似,因为BCFE是个正方形,AB为10厘米,BC为4厘米,所以AE=10-4=6厘米,所以△PMN与△PBC的相似比是:PM:PB=AE:AB=6:10=3:5;
所以它们的面积之比是相似比的平方:9:25,由此只要求得△PBC的面积即可解决问题.
所以它们的面积之比是相似比的平方:9:25,由此只要求得△PBC的面积即可解决问题.

解答:解:AD∥EF∥BC,所以△PMN与△PBC相似,
AB=10厘米,BC=4厘米,所以AE=10-4=6厘米,
所以△PMN与△PBC的相似比是:PM:PB=AE:AB=6:10=3:5;
则它们的面积之比是相似比的平方:9:25,
△PBC的面积为:4×10÷2=20(平方厘米),
所以阴影部分的面积为:20×9÷25=7.2(平方厘米),
答:阴影部分的面积是7.2平方厘米.
故答案为:7.2.
AB=10厘米,BC=4厘米,所以AE=10-4=6厘米,
所以△PMN与△PBC的相似比是:PM:PB=AE:AB=6:10=3:5;
则它们的面积之比是相似比的平方:9:25,
△PBC的面积为:4×10÷2=20(平方厘米),
所以阴影部分的面积为:20×9÷25=7.2(平方厘米),
答:阴影部分的面积是7.2平方厘米.
故答案为:7.2.
点评:此题考查了相似三角形的性质的灵活应用.

练习册系列答案
相关题目
 如图ABCD是个正方形,它的边长是4厘米,E、F分别是AB、BC的中点,图中阴影部分的面积是
如图ABCD是个正方形,它的边长是4厘米,E、F分别是AB、BC的中点,图中阴影部分的面积是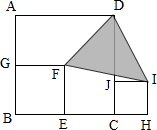 如图,有三个正方形ABCD,BEFG和CHIJ,其中正方形ABCD的边长是10,正方形BEFG的边长是6,那么三角形DFI的面积是
如图,有三个正方形ABCD,BEFG和CHIJ,其中正方形ABCD的边长是10,正方形BEFG的边长是6,那么三角形DFI的面积是 如图中,ABCD是边长为A的正方形,分别以AB、BC、CD、DA为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.
如图中,ABCD是边长为A的正方形,分别以AB、BC、CD、DA为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.
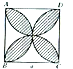 如图中,ABCD是边长为A的正方形,分别以AB、BC、CD、DA为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.
如图中,ABCD是边长为A的正方形,分别以AB、BC、CD、DA为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.