题目内容
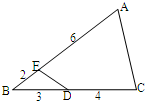如图所示，三角形ABC被线段DE分成三角形BDE和四边形ACDE两部分，问：三角形BDE的面积是四边形ACDE面积的几分之几？分析：先求△BDE的高占△ABC的几分之几，再利用三角形的面积求答案．
解答：解：根据图形可知：△BDE底边BD上的高：△ABCBC上的高=2：（2+6）=1：4，
S△BDE：S△ABC=（
×3×1）：（
×7×4）=3：28；
故：三角形BDE的面积是四边形ACDE面积的：3：（28-3）3：25=
．
S△BDE：S△ABC=（
| 1 |
| 2 |
| 1 |
| 2 |
故：三角形BDE的面积是四边形ACDE面积的：3：（28-3）3：25=
| 3 |
| 25 |
点评：把与不规则的图形的面积的比，转化成规则图形的面积的比，再找答案．
练习册系列答案
相关题目
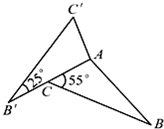如图所示，三角形ABC按照顺时针旋转一个角度后是三角形AB?C?，已知么∠B?=25°，∠ACB=55°．旋转中心是点
如图所示，三角形ABC是直角三角形，阴影①阴影的面积比阴影②的面积小28c㎡．AB长40cm，AC长是多少cm？
如图所示，三角形ABC中，D是AB边的三等分点，E是AC边的四等分点，已知三角形A DE的面积是1平方厘米．
如图所示，三角形ABC是直角三角形，AB是圆的直径，并且AB=20厘米，如果阴影（Ⅰ）比阴影（Ⅱ）的面积，大7厘米，那么BC的长度是