Question

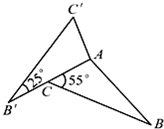如图所示，三角形ABC按照顺时针旋转一个角度后是三角形AB?C?，已知么∠B?=25°，∠ACB=55°．旋转中心是点

A

，旋转角度是

100°

．

Answer 1

分析：因三角形ABC按照顺时针旋转，旋转后的图形和原图形完全一样，通过观察可知，旋转中心是点A，∠B?=25°，所以∠C^′=∠ACB=55°，根据三角形的内角和是180°，可求出∠B^′AC^′的度数，就是旋转的度数．

解答：解：因∠C^′=∠ACB=55°
∠B^′AC^′=180°-∠B?-∠C^′
=180°-25°-55°
=100°
答：旋转中心是点A，旋转角度是100°．
故答案为：A，100°．

点评：本题的关键是根据旋转后的图形同原图形相同和三角形的内角和是180度的知识进行解答．