题目内容
如图所示的三角形ABC的三条边AB、BC、AC中，最长的
AC
AC
．分析：依据勾股定理即可求解．
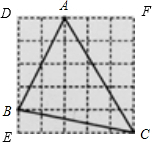
解答：解：如图所示，在正方形DECF中，除三角形ABC外，余下的三个三角形均为直角三角形，假设每个小正方形的边长为1厘米，则AD=2厘米、DB=4厘米、BE=1厘米、EC=5厘米、AF=3厘米、FC=
5厘米，由勾股定理可得：
AD2+DB2=AB2，
BE2+EC2=BC2，
AF2+FC2=AC2，
即：22+42=20=AB2，
12+52=26=BC2，
32+52=34=AC2，
所以在AB2、BC2、AC2中，AC2最大，则AC最长．
故此题答案为：AC．
5厘米，由勾股定理可得：
AD2+DB2=AB2，
BE2+EC2=BC2，
AF2+FC2=AC2，
即：22+42=20=AB2，
12+52=26=BC2，
32+52=34=AC2，
所以在AB2、BC2、AC2中，AC2最大，则AC最长．
故此题答案为：AC．
点评：此题主要考查勾股定理的运用．
练习册系列答案
综合自测系列答案
相关题目
如图所示，三角形ABC是直角三角形，阴影①阴影的面积比阴影②的面积小28c㎡．AB长40cm，AC长是多少cm？
如图所示，三角形ABC中，D是AB边的三等分点，E是AC边的四等分点，已知三角形A DE的面积是1平方厘米．
如图所示，三角形ABC是直角三角形，AB是圆的直径，并且AB=20厘米，如果阴影（Ⅰ）比阴影（Ⅱ）的面积，大7厘米，那么BC的长度是
把如图所示的直角三角形ABC沿着AB轴旋转一周，形成