题目内容
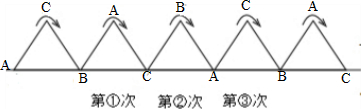
 等边三角形ABC的边长是3厘米,将其沿一条直线翻滚2002次(如图所示翻滚一次),求A点经过的总路程.
等边三角形ABC的边长是3厘米,将其沿一条直线翻滚2002次(如图所示翻滚一次),求A点经过的总路程.分析:如下图:翻转第一次A转动120°,它走的路程是圆心角是120°的圆弧;翻转第二次A转动120°,它走的路程是圆心角是120°的圆弧;翻转第三次A不转动,走的路程是0;三次翻转后回到原始状态;所以把转动3次看成一个周期,这一个周期里A一共行走了240°的圆弧,也就是
的圆的周长,根据圆的周长公式求出一组行走的路程,再求出2002次一共有多少个这样的一组,还余几,由此求解.
| 2 |
| 3 |

解答:解:每转动3次看成一个循环;
2002÷3=667…1;
每一组中A共转240°;
240°÷360°=
;
2×3.14×3×
,
=(2×3.14)×(3×
),
=6.28×2,
=12.56(厘米),
(12.56×667)+(12.56÷2),
=8377.52+6.28,
=8383.8(厘米);
答:A点经过的总路程8383.8厘米.
2002÷3=667…1;
每一组中A共转240°;
240°÷360°=
| 2 |
| 3 |
2×3.14×3×
| 2 |
| 3 |
=(2×3.14)×(3×
| 2 |
| 3 |
=6.28×2,
=12.56(厘米),
(12.56×667)+(12.56÷2),
=8377.52+6.28,
=8383.8(厘米);
答:A点经过的总路程8383.8厘米.
点评:本题是找规律题型,考查了等边三角形和旋转的性质.旋转变化前后,关键是找出一周期经过的路程,进而求出总路程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
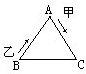 如图,等边三角形ABC的边长为100米,甲自A点,乙自B点同时出发,按顺时针方向沿着三角形的边行进.甲每分钟走60米,乙每分钟走90米,在过每个顶点时各人都因转弯而耽误10秒钟,那么乙在出发
如图,等边三角形ABC的边长为100米,甲自A点,乙自B点同时出发,按顺时针方向沿着三角形的边行进.甲每分钟走60米,乙每分钟走90米,在过每个顶点时各人都因转弯而耽误10秒钟,那么乙在出发 等边三角形ABC的边长90厘米,用折线把三角形分割成面积相等的四个三角形,那么CE和CF的长度和是多少厘米?
等边三角形ABC的边长90厘米,用折线把三角形分割成面积相等的四个三角形,那么CE和CF的长度和是多少厘米? 如图所示等边三角形ABC的边长为3厘米,弧CD是以A为为圆心,AC为半径的弧,同样弧DE是以B为圆心,BD为半径的弧,弧EF是以C为圆心,CE为半径的弧,交AC的延长线于点F,求这些圆弧的总长度.
如图所示等边三角形ABC的边长为3厘米,弧CD是以A为为圆心,AC为半径的弧,同样弧DE是以B为圆心,BD为半径的弧,弧EF是以C为圆心,CE为半径的弧,交AC的延长线于点F,求这些圆弧的总长度. 等边三角形ABC的边长是3厘米,将其沿一条直线翻滚2002次(如图所示翻滚一次),求A点经过的总路程.
等边三角形ABC的边长是3厘米,将其沿一条直线翻滚2002次(如图所示翻滚一次),求A点经过的总路程.