题目内容
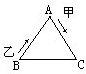 如图,等边三角形ABC的边长为100米,甲自A点,乙自B点同时出发,按顺时针方向沿着三角形的边行进.甲每分钟走60米,乙每分钟走90米,在过每个顶点时各人都因转弯而耽误10秒钟,那么乙在出发
如图,等边三角形ABC的边长为100米,甲自A点,乙自B点同时出发,按顺时针方向沿着三角形的边行进.甲每分钟走60米,乙每分钟走90米,在过每个顶点时各人都因转弯而耽误10秒钟,那么乙在出发220
220
秒之后追上甲.分析:甲的速度=60米/分=1米/秒,乙的速度=90米/分=1.5米/秒.根据题意可知,乙要追上甲,需要多走100米还要多转一个转弯,但在转弯处还要耽误10秒钟,此时甲又多走出10米,所以甲、乙的距离差为(100+10)=110米;由此可知,乙追上甲时共需时间:110÷(1.5-1)=220(秒).
解答:解:60米/分=1米/秒,90米/分=1.5米/秒,
(100+10)÷(1.5-1),
=110+0.5,
=220(秒);
答:乙在出发220秒之后追上甲.
故答案为:220.
(100+10)÷(1.5-1),
=110+0.5,
=220(秒);
答:乙在出发220秒之后追上甲.
故答案为:220.
点评:此题属于复杂的追及应用题,此类题的解答方法是根据“追及(拉开)路程÷(速度差)=追及(拉开)时间”,代入数值,计算即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图中由等边三角形ABO,AOD,DOC围成的等腰梯形,它的面积是1,又知M是AB的中点,那么△COM面积等于多少?
如图中由等边三角形ABO,AOD,DOC围成的等腰梯形,它的面积是1,又知M是AB的中点,那么△COM面积等于多少?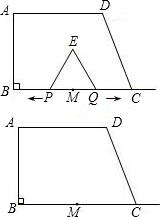
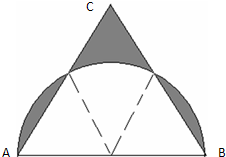 已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14)
已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14) 如图,已知△ABD与△BCD都是边长为3厘米的等边三角形,以A为圆心,AB长为半径画弧BD;以B为圆心,BC长为半径画弧CD,求阴影部分图形的周长.
如图,已知△ABD与△BCD都是边长为3厘米的等边三角形,以A为圆心,AB长为半径画弧BD;以B为圆心,BC长为半径画弧CD,求阴影部分图形的周长.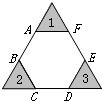 如图,六边形ABCDEF的各边都相等,每个内角都是120°,AB、CD、EF每两条线的延长线交于一点,三个交点构成一个等边三角形,若阴影部分的面积和是S,则六边形ABCDEF的面积为
如图,六边形ABCDEF的各边都相等,每个内角都是120°,AB、CD、EF每两条线的延长线交于一点,三个交点构成一个等边三角形,若阴影部分的面积和是S,则六边形ABCDEF的面积为