题目内容
 等边三角形ABC的边长90厘米,用折线把三角形分割成面积相等的四个三角形,那么CE和CF的长度和是多少厘米?
等边三角形ABC的边长90厘米,用折线把三角形分割成面积相等的四个三角形,那么CE和CF的长度和是多少厘米?分析:根据三角形ABC的边长都是90厘米,用折线把三角形分割成面积相等的四个三角形,可得△ABD和△BDC的面积之比是1:3,根据三角形的高一定时,面积与底成正比的性质可得:AD:DC=1:3;因为AC=90厘米,即可求得CD=90×
=67.5厘米;同理即可求得CF和CE的长度.
| 3 |
| 4 |
解答:解:根据题干可得:△ABD=△BDE=△DEF=△EFC
(1)△ABD和△BDC的面积之比是1:3,根据三角形的高一定时,面积与底成正比的性质可得:AD:DC=1:3;因为AC=90厘米,即可求得CD=90×
=67.5厘米;
(2)△DEF和△DFC的面积之比是1:1,根据三角形的高一定时,面积与底成正比的性质可得:DF:FC=1:1;因为DC=67.5厘米,即可求得CF=67.5×
=33.75厘米;
(3)△BDE和△EDC的面积之比是1:2,根据三角形的高一定时,面积与底成正比的性质可得:BE:EC=1:2;因为BC=90厘米,即可求得CE=90×
=60厘米;
答:CF的长度为33.75厘米,CE的长度为60厘米.
(1)△ABD和△BDC的面积之比是1:3,根据三角形的高一定时,面积与底成正比的性质可得:AD:DC=1:3;因为AC=90厘米,即可求得CD=90×
| 3 |
| 4 |
(2)△DEF和△DFC的面积之比是1:1,根据三角形的高一定时,面积与底成正比的性质可得:DF:FC=1:1;因为DC=67.5厘米,即可求得CF=67.5×
| 1 |
| 2 |
(3)△BDE和△EDC的面积之比是1:2,根据三角形的高一定时,面积与底成正比的性质可得:BE:EC=1:2;因为BC=90厘米,即可求得CE=90×
| 2 |
| 3 |
答:CF的长度为33.75厘米,CE的长度为60厘米.
点评:此题反复考查了三角形的高一定时,三角形的面积与底成正比的性质的灵活应用.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
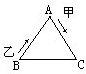 如图,等边三角形ABC的边长为100米,甲自A点,乙自B点同时出发,按顺时针方向沿着三角形的边行进.甲每分钟走60米,乙每分钟走90米,在过每个顶点时各人都因转弯而耽误10秒钟,那么乙在出发
如图,等边三角形ABC的边长为100米,甲自A点,乙自B点同时出发,按顺时针方向沿着三角形的边行进.甲每分钟走60米,乙每分钟走90米,在过每个顶点时各人都因转弯而耽误10秒钟,那么乙在出发 等边三角形ABC的边长是3厘米,将其沿一条直线翻滚2002次(如图所示翻滚一次),求A点经过的总路程.
等边三角形ABC的边长是3厘米,将其沿一条直线翻滚2002次(如图所示翻滚一次),求A点经过的总路程. 如图所示等边三角形ABC的边长为3厘米,弧CD是以A为为圆心,AC为半径的弧,同样弧DE是以B为圆心,BD为半径的弧,弧EF是以C为圆心,CE为半径的弧,交AC的延长线于点F,求这些圆弧的总长度.
如图所示等边三角形ABC的边长为3厘米,弧CD是以A为为圆心,AC为半径的弧,同样弧DE是以B为圆心,BD为半径的弧,弧EF是以C为圆心,CE为半径的弧,交AC的延长线于点F,求这些圆弧的总长度. 等边三角形ABC的边长是3厘米,将其沿一条直线翻滚2002次(如图所示翻滚一次),求A点经过的总路程.
等边三角形ABC的边长是3厘米,将其沿一条直线翻滚2002次(如图所示翻滚一次),求A点经过的总路程.