题目内容
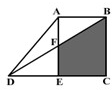在直角梯形ABCD中，三角形ABD的面积是15平方厘米，AF=4厘米，AB=3厘米．
那么图中阴影部分的面积是________平方厘米．
24
分析：根据图示可知，阴影部分的图形为直角梯形，先根据三角形的面积公式可用三角形的面积乘2除以三角形的底3厘米就可计算出三角形的高即AE的高，因为BC=AE，EC=AB=3厘米，EF=AE-AF，最后再根据梯形的面积公式进行计算即可得到答案．
解答：AE的长为：15×2÷3=10（厘米），
EF的长为：10-4=6（厘米），
阴影部分的面积为：（6+10）×3÷2
=16×3÷2，
=48÷2，
=24（平方厘米）；
答：阴影部分的面积为24平方厘米．
故答案为：24．
点评：解答此题的关键是确定三角形ABD的高，然后再根据梯形的面积公式（上底+下底）×高÷2进行计算即可．
分析：根据图示可知，阴影部分的图形为直角梯形，先根据三角形的面积公式可用三角形的面积乘2除以三角形的底3厘米就可计算出三角形的高即AE的高，因为BC=AE，EC=AB=3厘米，EF=AE-AF，最后再根据梯形的面积公式进行计算即可得到答案．
解答：AE的长为：15×2÷3=10（厘米），
EF的长为：10-4=6（厘米），
阴影部分的面积为：（6+10）×3÷2
=16×3÷2，
=48÷2，
=24（平方厘米）；
答：阴影部分的面积为24平方厘米．
故答案为：24．
点评：解答此题的关键是确定三角形ABD的高，然后再根据梯形的面积公式（上底+下底）×高÷2进行计算即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在直角梯形ABCD中，三角形ABD的面积是15平方厘米，AF=4厘米，AB=3厘米．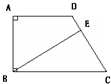
如图，在直角梯形ABCD中，已知AD=3cm，AB=4cm，CD=5cm，BC=6cm，BE将梯形分成面积相等的两部分．问DE的长是多厘米？
如图，在直角梯形ABCD中，AD∥BC，CD⊥BC，E为BC边上的点，将直角梯形ABCD沿对角线BD折叠，使△ABD与△EBD重合（如图中的阴影部分）．若∠A=120°，AB=4cm，求梯形ABCD的高CD．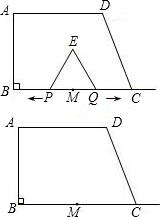
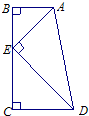如图，在直角梯形ABCD中，三角形ABE和三角形CDE都是等腰直角三角形，且BC=20厘米，那么直角梯形ABCD的面积是