题目内容
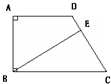
 如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点,将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中的阴影部分).若∠A=120°,AB=4cm,求梯形ABCD的高CD.
如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点,将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中的阴影部分).若∠A=120°,AB=4cm,求梯形ABCD的高CD.分析:根据折叠可以得到它们的对应边相等,对应角相等.从而发现30°的Rt△CDE,根据折叠可知四边形ABED是菱形,得到DE=AB=4,再进行计算.
解答:解:由题意△ABD与△EBD关于对角线BD对称,
所以∠BED=∠A=120°,
因为点E在BC边上,
所以∠DEC=60°,
因为AD∥BC,
所以∠ABC=60°,
所以∠ABC=∠DEC,
所以AB∥DE,
所以四边形ABED为平行四边形,
所以DE=AB=4cm,
所以CD=sin60°×DE=
×4=2
(厘米)
所以∠BED=∠A=120°,
因为点E在BC边上,
所以∠DEC=60°,
因为AD∥BC,
所以∠ABC=60°,
所以∠ABC=∠DEC,
所以AB∥DE,
所以四边形ABED为平行四边形,
所以DE=AB=4cm,
所以CD=sin60°×DE=
| ||
| 2 |
| 3 |
点评:根据折叠的意义,能够从折叠中发现它们的对应边相等,对应角相等.

练习册系列答案
相关题目
 如图,在直角梯形ABCD中,已知AD=3cm,AB=4cm,CD=5cm,BC=6cm,BE将梯形分成面积相等的两部分.问DE的长是多厘米?
如图,在直角梯形ABCD中,已知AD=3cm,AB=4cm,CD=5cm,BC=6cm,BE将梯形分成面积相等的两部分.问DE的长是多厘米?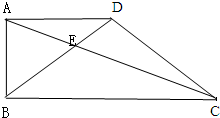 (2011?长春模拟)如图,在直角梯形ABCD中,上底AD的长是12厘米,高AB长9厘米,BE=2ED,底边BC长多少厘米?
(2011?长春模拟)如图,在直角梯形ABCD中,上底AD的长是12厘米,高AB长9厘米,BE=2ED,底边BC长多少厘米?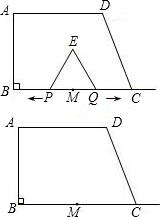
 如图,在直角梯形ABCD中,已知AD=3cm,AB=4cm,CD=5cm,BC=6cm,BE将梯形分成面积相等的两部分.问DE的长是多厘米?
如图,在直角梯形ABCD中,已知AD=3cm,AB=4cm,CD=5cm,BC=6cm,BE将梯形分成面积相等的两部分.问DE的长是多厘米?