题目内容
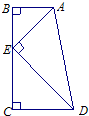如图，在直角梯形ABCD中，三角形ABE和三角形CDE都是等腰直角三角形，且BC=20厘米，那么直角梯形ABCD的面积是分析：梯形面积为（上底+下底）×高÷2，因为AB=BE，CD=CE，所以AB+CD=BE+CE=BC=20cm，即两个等腰直角三角形边长之和为梯形的高，梯形的面积为20×20÷2=200（cm2）．
解答：解：因为AB=BE，CD=CE，所以AB+CD=BE+CE=BC=20cm，即两个等腰直角三角形边长之和为梯形的高，
梯形的面积为20×20÷2=200（cm2）．
答：梯形的面积是200平方厘米．
故答案为：200．
梯形的面积为20×20÷2=200（cm2）．
答：梯形的面积是200平方厘米．
故答案为：200．
点评：解答此题的关键是根据等腰直角三角形的性质求出梯形的上下底和高的值．
练习册系列答案
相关题目
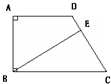如图，在直角梯形ABCD中，已知AD=3cm，AB=4cm，CD=5cm，BC=6cm，BE将梯形分成面积相等的两部分．问DE的长是多厘米？
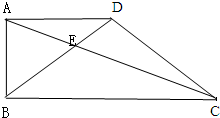（2011?长春模拟）如图，在直角梯形ABCD中，上底AD的长是12厘米，高AB长9厘米，BE=2ED，底边BC长多少厘米？
如图，在直角梯形ABCD中，AD∥BC，CD⊥BC，E为BC边上的点，将直角梯形ABCD沿对角线BD折叠，使△ABD与△EBD重合（如图中的阴影部分）．若∠A=120°，AB=4cm，求梯形ABCD的高CD．
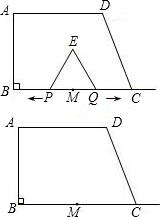
如图，在直角梯形ABCD中，已知AD=3cm，AB=4cm，CD=5cm，BC=6cm，BE将梯形分成面积相等的两部分．问DE的长是多厘米？