题目内容
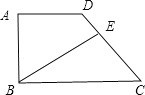
【题目】如果所示的直角梯形ABCD中，AD=3厘米，AB=4厘米，BC=6厘米，BE将梯形分成面积相等的两部分，DE：EC= ： ．
【答案】1，3．
【解析】
试题分析：连接BD，△ABD是直角三角形，面积=
ABAD，直角梯形ABCD的面积=（AD+BC）AB，因为“BE将梯形分成面积相等的两部分”，所以△BCE的面积=直角梯形ABCD的面积，△BED的面积=直角梯形ABCD的面积﹣△ABD的面积，因为△BCE和△BED等高，所以底边DE：EC=△BED的面积：△BCE的面积，带入数据，即可得解．
解：
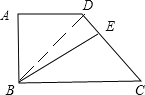
直角梯形ABCD的面积=（AD+BC）AB，
=（3+6）×4÷2，
=18（平方厘米）；
△ABD的面积=ABAD=3×4÷2=6（平方厘米），
因为△BCE和△BED等高，
所以底边DE：EC=△BED的面积：△BCE的面积，
=（18÷2﹣6）：（18÷2），
=3：9，
=1：3；
答：DE：EC=1：3；
练习册系列答案
阅读快车系列答案
相关题目
