题目内容
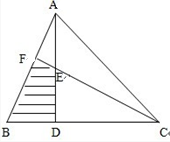 如图,在三角形ABC中,BD:DC=1:2,E为AD的中点,若三角形ABC的面积为120平方厘米,则阴影部分的面积是多少平方厘米?
如图,在三角形ABC中,BD:DC=1:2,E为AD的中点,若三角形ABC的面积为120平方厘米,则阴影部分的面积是多少平方厘米?分析:(1)观察图形可知:BD:DC=1:2,所以三角形ABD=
三角形ADC=
三角形ABC=120×
=40(平方厘米),E为AD的中点,所以三角形AEC=三角形DEC=
三角形ADC,由此可得:三角形ABD=三角形DEC=三角形AEC=40(平方厘米),
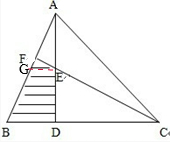
(2)再利用平行线分线段成比例和相似三角形的性质来推算,此题要添加辅助线,即过点E作EG∥BC,交AB于一点G.根据平行线分线段成比例的性质,得出FE与EC的比,求出三角形AFE的面积即可解答.如图:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
(2)再利用平行线分线段成比例和相似三角形的性质来推算,此题要添加辅助线,即过点E作EG∥BC,交AB于一点G.根据平行线分线段成比例的性质,得出FE与EC的比,求出三角形AFE的面积即可解答.如图:

解答:解:BD:DC=1:2,所以三角形ABD=
三角形ADC=
三角形ABC=120×
=40(平方厘米),
E为AD的中点,所以三角形AEC=三角形DEC=
三角形ADC,
由此可得:三角形ABD=三角形DEC=三角形AEC=40(平方厘米),
过点E作EG∥BC,交AB于一点G,因为E是AD的中点,
所以GE:BD=1:2,
又因为BD:DC=1:2,所以BD:BC=1:3=2:6,
则GE:BC=1:6,
因为EG∥BC,所以FE:FC=GE:BC=1:6,
则FE:EC=1:5,
所以三角形AFE的面积是:40×1÷5=8(平方厘米),
则阴影部分的面积是:40-8=32(平方厘米),
答:阴影部分的面积是32平方厘米.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
E为AD的中点,所以三角形AEC=三角形DEC=
| 1 |
| 2 |
由此可得:三角形ABD=三角形DEC=三角形AEC=40(平方厘米),
过点E作EG∥BC,交AB于一点G,因为E是AD的中点,
所以GE:BD=1:2,
又因为BD:DC=1:2,所以BD:BC=1:3=2:6,
则GE:BC=1:6,
因为EG∥BC,所以FE:FC=GE:BC=1:6,
则FE:EC=1:5,
所以三角形AFE的面积是:40×1÷5=8(平方厘米),
则阴影部分的面积是:40-8=32(平方厘米),
答:阴影部分的面积是32平方厘米.
点评:此题考查平行线分线段成比例的性质和高一定时,三角形的面积与底成正比例的性质的灵活应用,考查了学生分析图形解决问题的能力.

练习册系列答案
相关题目
 如图,在三角形ABC中,BD:DC=1:2,AE=ED,则AF:FC=( )
如图,在三角形ABC中,BD:DC=1:2,AE=ED,则AF:FC=( ) 如图:在三角形ABC中,BD=
如图:在三角形ABC中,BD= 如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的( ) 倍.
如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的( ) 倍. 如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的
如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的 如图,在三角形ABC中,D、E为两个三等分点,F为AB的中点,若△EDF的面积是12平方厘米,则△ABC的面积是( )平方厘米.
如图,在三角形ABC中,D、E为两个三等分点,F为AB的中点,若△EDF的面积是12平方厘米,则△ABC的面积是( )平方厘米.