题目内容
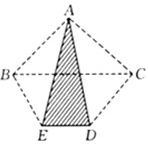
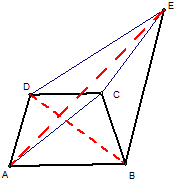 如图,已知梯形ABCD的面积为5,DA与EB平行,ED与CA平行,求四边形EDAC的面积.
如图,已知梯形ABCD的面积为5,DA与EB平行,ED与CA平行,求四边形EDAC的面积.分析:连接EA、DB,根据平行线间的距离处处相等,和等底等高的三角形的面积相等,可得△EDC的面积=△EDA的面积、△EDA的面积=△DAB的面积、△DAB的面积=△CAB的面积;据此可得△EDC的面积=△CAB的面积;据此可得四边形EDAC的面积=△EDC的面积+△CDA的面积=△CAB的面积+△CDA的面积=梯形ABCD的面积=5.
解答:解:连接EA、DB,
因为ED∥CA,所以△EDC的面积=△EDA的面积,
因为DA∥EB,所以△EDA的面积=△DAB的面积,
因为DC∥AB,所以△DAB的面积=△CAB的面积;
据此可得△EDC的面积=△CAB的面积;
所以四边形EDAC的面积=△EDC的面积+△CDA的面积=△CAB的面积+△CDA的面积=梯形ABCD的面积=5.
答:四边形EDAC的面积是5.
因为ED∥CA,所以△EDC的面积=△EDA的面积,
因为DA∥EB,所以△EDA的面积=△DAB的面积,
因为DC∥AB,所以△DAB的面积=△CAB的面积;
据此可得△EDC的面积=△CAB的面积;
所以四边形EDAC的面积=△EDC的面积+△CDA的面积=△CAB的面积+△CDA的面积=梯形ABCD的面积=5.
答:四边形EDAC的面积是5.
点评:此题主要考查平行线和等底等高的三角形的面积相等的性质,解答此题的关键是把四边形EDAC的面积转移到已知的梯形中.

练习册系列答案
相关题目
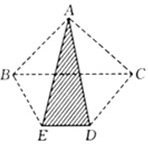 (2004?武汉)如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是
(2004?武汉)如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是 如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积?
如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积?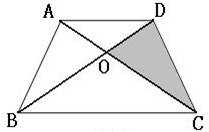 如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积?
如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积? 如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是________.
如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是________.