题目内容
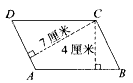
 如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积?
如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积?分析:根据三角形ABC的面积为5平方厘米,BC=5厘米,可以求出三角形ABC的高,即三角形ADC的高,由此即可求出三角形ACD的面积,再根据三角形AOD与三角形BOC相似,得出对应边的比等于对应高的比,求出三角形AOD的高,进而求出三角形AOD的面积,继而求出阴影部分的面积.
解答:解:ABC高是:5×2÷5=2(厘米),
ACD面积是:2×2÷2=2(平方厘米),
因为三角形AOD与三角形BOC相似,
设三角形AOD的高为x厘米,则三角形BOC的高为2-x厘米,
所以x:(2-x)=2:5,
5x=4-2x,
7x=4,
x=
,
三角形AOD的面积是:2×
÷2=
(平方厘米),
三角形COD面积是:2-
=
(平方厘米),
答:阴影部分的面积是
平方厘米.
ACD面积是:2×2÷2=2(平方厘米),
因为三角形AOD与三角形BOC相似,
设三角形AOD的高为x厘米,则三角形BOC的高为2-x厘米,
所以x:(2-x)=2:5,
5x=4-2x,
7x=4,
x=
| 4 |
| 7 |
三角形AOD的面积是:2×
| 4 |
| 7 |
| 4 |
| 7 |
三角形COD面积是:2-
| 4 |
| 7 |
| 10 |
| 7 |
答:阴影部分的面积是
| 10 |
| 7 |
点评:本题主要是灵活利用三角形的面积公式与三角形的相似性解决问题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的
如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的 如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.
如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.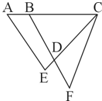 如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的________倍.
如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的________倍.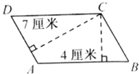 如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.
如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.