题目内容
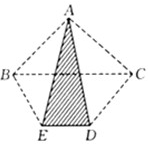 (2004?武汉)如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是
(2004?武汉)如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是3
3
.分析:要求△ADE的面积,它的底和高无法求出具体数量,只能从图形中的关系去考虑,因为BC是DE的2倍,△ADE的高是△ABC的高与梯形BCDE的高的和,所以设DE=x,则BC=2x,设△ABC的高为h1,梯形BCDE的高为h2;则
×2x×h1=2,
×(2x+x)×h2=6;可得出x×h1=2,x×h2=4;进而得出x×h1+x×h2=x×(h1+h2)=6;所以△ADE的面积为
×x×(h1+h2)=3.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设DE=x,则BC=2x;
设△ABC的高为h1,梯形BCDE的高为h2;
则
×2x×h1=2,
×(2x+x)×h2=6;
所以x×h1=2,x×h2=4;
所以△ADE的面积=
×x×(h1+h2)=3.
设△ABC的高为h1,梯形BCDE的高为h2;
则
| 1 |
| 2 |
| 1 |
| 2 |
所以x×h1=2,x×h2=4;
所以△ADE的面积=
| 1 |
| 2 |
点评:此题求三角形的面积,如果按常规思路无法求出底和高,所以要从图形中的关系去考虑,用含有字母的式子表示三角形的面积公式,逐步解决问题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 (2004?武汉)如图是学校一个正方形花圃的设计图,图中阴影部分是花圃,空白部分是草坪.求花圃的面积是多少平方米?
(2004?武汉)如图是学校一个正方形花圃的设计图,图中阴影部分是花圃,空白部分是草坪.求花圃的面积是多少平方米? (2004?武汉)胡裁缝加工一批服装的情况如图.已知他加工一件童装、一条裤子和一件上衣所需要时间的比是1:2:3,他每天加工2件童装、3条裤子和4件上衣.请问,他加工完这批服装用了多少天?
(2004?武汉)胡裁缝加工一批服装的情况如图.已知他加工一件童装、一条裤子和一件上衣所需要时间的比是1:2:3,他每天加工2件童装、3条裤子和4件上衣.请问,他加工完这批服装用了多少天? (2004?武汉)算“24点”是我国传统的数学游戏.这里有四张扑克牌(如图),用它们凑成“24点”的算式是
(2004?武汉)算“24点”是我国传统的数学游戏.这里有四张扑克牌(如图),用它们凑成“24点”的算式是 (2004?武汉)如图,直角三角形的三边为3,4,5,EF,EG,ED垂直于AB,BC,CA,且EF=EG=ED,求EF.
(2004?武汉)如图,直角三角形的三边为3,4,5,EF,EG,ED垂直于AB,BC,CA,且EF=EG=ED,求EF.