��Ŀ����
����Ŀ�������Ѿ�֪�������ε��ڽǺ��� 180�㣬���ǿ��������֪ʶ����ı��Ρ�����Ρ��������ڽǺ͵Ķ���������̽��������ε��ڽǺͣ���ƽ���ڣ�������������ͬһֱ���ϵ��߶� ��β˳��������ɵķ��ͼ�ν�������Σ�����ε��ڽǡ��ڽǺ͵ĺ�������������ͬ��
���Ķ������е����ݲ���գ�
ͼ �� | �ֳ������εĸ��� | �ڽǺ͵Ķ��� |
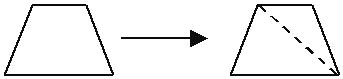
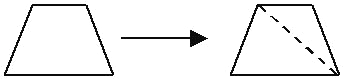
| �ı��ο��Էֳ� 2 �������� | �ı��ε��ڽǺ�=180���2 |
=360�� | ||
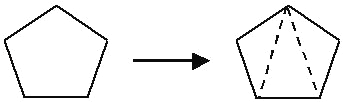
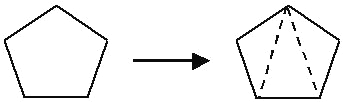
| ����οɷֳ� 3 �������� | ����ε��ڽǺ�=180���3 |
=540�� | ||
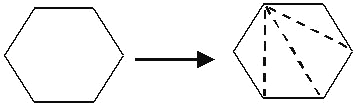
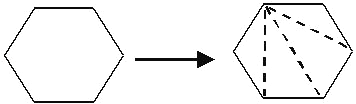
| �����οɷֳ� �������� | �����ε��ڽǺ�= |
= | ||
�ڸ����ı��Ρ�����Ρ��������ڽǺ͵ļ��㷽�������ɳ� n ���ε��ڽǺͣ�
n ���ε��ڽǺ�= ���ú�����ĸ n ��ʽ�ӱ�ʾ��
����ij����ε��ڽǺ��� 1440�㣬���â��еĽ��ۼ����������εı�����
���𰸡�4��180���4=720�㣬1180�����n��2����
��������
����������٢ڸ��ݹ�ͬһ���������ĶԽ��߰Ѷ���ηֳɵ������εĸ����Ĺ��ɣ������������ε��ڽǺ͵���180�㼴���Ƴ�����ε��ڽǺ�ʽ��
�۸����ڽǺ�ʽ������ⷽ�̼��ɣ�
�⣺����Ϊ�ı��ο��Էֳ����������Σ����������Էֳ�3�������Σ��������ƣ��������ο��Էֳ�4�������Σ��������ڽǺ���4��180��=720�ȣ����±���
ͼ �� | �ֳ������εĸ��� | �ڽǺ͵Ķ��� |
| �ı��ο��Էֳ�2�������� | �ı��ε��ڽǺ�=180���2 |
=360�� | ||
| ����οɷֳ�3�������� | ����ε��ڽǺ�=180���3 |
=540�� | ||
| �����οɷֳ�4�������� | �����ε��ڽǺ�=180���4 |
=720�� | ||
����Ϊ1�������ε��ڽǺ���1��180�㣬�ı��ο��Էֳ����������Σ������ڽǺ���2��180�㣻
���������Էֳ�3�������Σ������ڽǺ���3��180�㣬
�������ƣ��������ο��Էֳ�4�������Σ������ڽǺ���4��180�㣻
�Դ�����n���ο��Էֳ�n��2�������Σ�����n���ε��ڽǺ͵��ڣ�n��2��180�㣮
�ۣ�n��2��180��=1440��
��n��2��180���180��=1440���180��
n��2=6
n��2+2=6+2
n=8
���������εı�����8��
�ʴ�Ϊ��4��180���4=720�㣬1180�����n��2����

 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�