题目内容
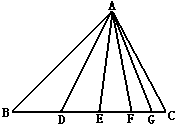 如图,在△ABC中,BD=5,DE=4,EF=3,FG=2,GC=1,若图中所有三角形面积的和为210平方厘米,那么△ABC的面积为________平方厘米.
如图,在△ABC中,BD=5,DE=4,EF=3,FG=2,GC=1,若图中所有三角形面积的和为210平方厘米,那么△ABC的面积为________平方厘米.
30
分析:每个小三角形和另外1个、2个、3个、4个三角形都能组成三角形,连同这5个小三角形及△ABC一共是5×4×3×2×1=15(个)三角形,这15个三角形又是由5个底边是5厘米、8个底边是4厘米、9个底边是3厘米、8个底边是2厘米、5个底边是1厘米的三角形组成的,这些三角形可以看作是底边为5×5+4×8+3×9+2×8+1×5=25+32+27+16+5=105(厘米),与三角形ABC等高的一个大三角形,又知这些三角形的和为210平方厘米,210平方厘米÷105=2(平方厘米),也就是底为1厘米的三角形的面积是2平方厘米,据此可求出底边为5厘米、4厘米、3厘米、2厘米、1厘米的三角形的面积,这几个三角形的面积的和就是△ABC的面积.
解答:如图,
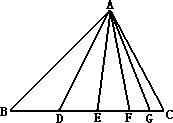
图中有5×4×3×2×1=15(个)三角形,
这些三角形又是由5个底边是5厘米、8个底边是4厘米、9个底边是3厘米、8个底边是2厘米、5个底边是1厘米的三角形组成的,
这些三角形可以看作是底边为5×5+4×8+3×9+2×8+1×5=25+32+27+16+5=105(厘米),与三角形ABC等高的一个大三角形,
210÷105=2(平方厘米),
△ABC的面积是:2×(5+4+3+2+1)
=2×15
=30(平方厘米);
故答案为:30
点评:本题是考查组合图形的面积,解答此题的关键是弄清图中一共有多少个三形,这些三角形又是由哪些三角形组成的,把这些三角形看作一个大三角形,底是1厘米的三角形的面积是多少.
分析:每个小三角形和另外1个、2个、3个、4个三角形都能组成三角形,连同这5个小三角形及△ABC一共是5×4×3×2×1=15(个)三角形,这15个三角形又是由5个底边是5厘米、8个底边是4厘米、9个底边是3厘米、8个底边是2厘米、5个底边是1厘米的三角形组成的,这些三角形可以看作是底边为5×5+4×8+3×9+2×8+1×5=25+32+27+16+5=105(厘米),与三角形ABC等高的一个大三角形,又知这些三角形的和为210平方厘米,210平方厘米÷105=2(平方厘米),也就是底为1厘米的三角形的面积是2平方厘米,据此可求出底边为5厘米、4厘米、3厘米、2厘米、1厘米的三角形的面积,这几个三角形的面积的和就是△ABC的面积.
解答:如图,

图中有5×4×3×2×1=15(个)三角形,
这些三角形又是由5个底边是5厘米、8个底边是4厘米、9个底边是3厘米、8个底边是2厘米、5个底边是1厘米的三角形组成的,
这些三角形可以看作是底边为5×5+4×8+3×9+2×8+1×5=25+32+27+16+5=105(厘米),与三角形ABC等高的一个大三角形,
210÷105=2(平方厘米),
△ABC的面积是:2×(5+4+3+2+1)
=2×15
=30(平方厘米);
故答案为:30
点评:本题是考查组合图形的面积,解答此题的关键是弄清图中一共有多少个三形,这些三角形又是由哪些三角形组成的,把这些三角形看作一个大三角形,底是1厘米的三角形的面积是多少.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图,在△ABC中,D为BC边上任一点,AE=
如图,在△ABC中,D为BC边上任一点,AE= 如图,在△ABC中,两条角平分线CD、EF相交于F,∠A=60°,则∠DFE=
如图,在△ABC中,两条角平分线CD、EF相交于F,∠A=60°,则∠DFE= (2013?北京模拟)如图,在△ABC中,AD=
(2013?北京模拟)如图,在△ABC中,AD= 如图,在△ABC中,E、D、F分别为AD、BC、AB的中点,BD=DE=EC,BF=FA,△EDF的面积是1,那么△ABC的面积是多少?
如图,在△ABC中,E、D、F分别为AD、BC、AB的中点,BD=DE=EC,BF=FA,△EDF的面积是1,那么△ABC的面积是多少?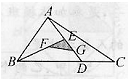 如图,在△ABC中,
如图,在△ABC中,