题目内容
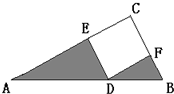 如图,三角形ABC是直角三角形,四边形EDFC是正方形,两个阴影三角形的面积之和是32平方厘米,AD:DB=4:1,求AD的长度.
如图,三角形ABC是直角三角形,四边形EDFC是正方形,两个阴影三角形的面积之和是32平方厘米,AD:DB=4:1,求AD的长度.分析:我们运用两直线平行公理求出AE与EC,BF与FC的数量关系,并用正方形的边长表示出来,再运用勾股定理在直角三角形AED中进一步求出AD的长度.
解答:解:因为三角形ABC是直角三角形,四边形EDFC是正方形,
所以DE∥BC,DF∥AC,DE=EC=CF=FD,
设正方形EDFC的边长是x,
因为AD:DB=4:1,
所以BF=
FC=
x,AE=4EC=4x,
两个阴影三角形的面积之和是32平方厘米,
BF×FD+
DE×AE=32,
即,
(
x×x)+
(x×4x)=32,
x2+2x2=32,
x2=32,
17x2=32×8,
17x2=162
在直角三角形ADE中,
AD2=AE2+ED2,
=(4x)2+x2,
=17x2,
AD2=162,
AD=16;
所以AD的长度是16厘米.
答:AD的长度是16厘米.
所以DE∥BC,DF∥AC,DE=EC=CF=FD,
设正方形EDFC的边长是x,
因为AD:DB=4:1,
所以BF=
| 1 |
| 4 |
| 1 |
| 4 |
两个阴影三角形的面积之和是32平方厘米,
| 1 |
| 2 |
| 1 |
| 2 |
即,
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 17 |
| 8 |
17x2=32×8,
17x2=162
在直角三角形ADE中,
AD2=AE2+ED2,
=(4x)2+x2,
=17x2,
AD2=162,
AD=16;
所以AD的长度是16厘米.
答:AD的长度是16厘米.
点评:本题考查了直线平行公理及勾股定理的运用,考查了学生灵活解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图:三角形ABC是直角三角形,AC是圆的半径且AC=10cm.阴影Y的面积比阴影X的面积小32平方厘米.求BD的长.
如图:三角形ABC是直角三角形,AC是圆的半径且AC=10cm.阴影Y的面积比阴影X的面积小32平方厘米.求BD的长. (2012?中山市模拟)如图,三角形ABC是面积为46.8平方厘米的等边三角形,ABCD是平行四边形,圆的半径是6厘米,求阴影部分的面积.
(2012?中山市模拟)如图,三角形ABC是面积为46.8平方厘米的等边三角形,ABCD是平行四边形,圆的半径是6厘米,求阴影部分的面积. (2012?福州)如图:三角形ABC是等腰直角三角形,直角边为4厘米,求阴影部分面积.
(2012?福州)如图:三角形ABC是等腰直角三角形,直角边为4厘米,求阴影部分面积.
 如图,三角形ABC是一个等腰三角形,AC=BC,已知∠ACD=130°,
如图,三角形ABC是一个等腰三角形,AC=BC,已知∠ACD=130°,