题目内容
【题目】探索规律．
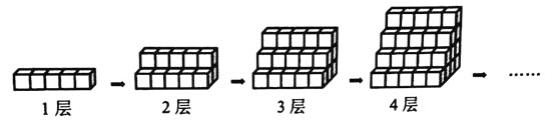
（1）按小方块的摆放规律把表格填写完整．
层数 | 1 | 2 | 3 | 4 | … | 7 | … | n |
方块个数 | 5 | 15 | 30 | （____） | … | （____） | … | （____） |
（2）当所用的小方块达到330个时，搭成的台阶共有________层．
【答案】50 140 （1+2+3+4+……+n）×5或（1+n）×n×
或1×5+2×5+3×5++n×5 11
【解析】
（1）观察图形排列可得规律：当小方块摆放n层时，方块的个数是：（1+n）×n×
；
（2）根据题意，要求搭成的台阶一共有几层，直接将数据代入字母式子中求值，据此解答．
（2）（1+n）×n×=330
（1+n）×n×5=330×2
（1+n）×n×5÷5=660÷5
（1+n）×n=132
因为11×12=132，所以n=11.
练习册系列答案
相关题目
