题目内容
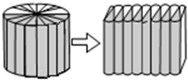 如图,把一个圆柱切拼成一个近似的长方体,这时长方体的表面积比原来增加了12平方厘米.如果截成两个小圆柱它的表面积增加了6.28平方厘米,求原来圆柱体的表面积
如图,把一个圆柱切拼成一个近似的长方体,这时长方体的表面积比原来增加了12平方厘米.如果截成两个小圆柱它的表面积增加了6.28平方厘米,求原来圆柱体的表面积43.96平方厘米
43.96平方厘米
.分析:(1)根据“如果截成两个小圆柱它的表面积增加了6.28平方厘米”,可以求出这个圆柱的底面积是6.28÷2=3.14平方厘米,从而求出这个圆柱的底面半径;
(2)将一个圆柱切开后拼成一个近似的长方体后,表面积比圆柱多了两个长方形的面积,这两个长方形的长是圆柱的高,宽与圆柱的底面半径相等;已知表面积增加了12平方厘米,就可求出高,进而再求出圆柱的表面积即可.
(2)将一个圆柱切开后拼成一个近似的长方体后,表面积比圆柱多了两个长方形的面积,这两个长方形的长是圆柱的高,宽与圆柱的底面半径相等;已知表面积增加了12平方厘米,就可求出高,进而再求出圆柱的表面积即可.
解答:解:圆柱的底面积是:6.28÷2=3.14(平方厘米),
3.14÷3.14=1,因为1×1=1,
所以这个圆柱的底面半径是1厘米,
所以圆柱的高是:12÷2÷1=6(厘米),
所以圆柱的表面积是:3.14×2+3.14×1×2×6,
=6.28+37.68,
=43.96(平方厘米),
答:圆柱的表面积是43.96平方厘米.
故答案为:43.96平方厘米.
3.14÷3.14=1,因为1×1=1,
所以这个圆柱的底面半径是1厘米,
所以圆柱的高是:12÷2÷1=6(厘米),
所以圆柱的表面积是:3.14×2+3.14×1×2×6,
=6.28+37.68,
=43.96(平方厘米),
答:圆柱的表面积是43.96平方厘米.
故答案为:43.96平方厘米.
点评:此题考查了圆柱的表面积公式的计算应用,根据两种不同的切割特点分别求出圆柱的底面半径和高是本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
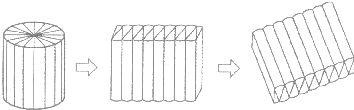 如图,把一个圆柱体切拼成一个近似长方体,再把这个长方体侧放,你就会有一种巧妙的方法算出圆柱的体积.如果圆柱的底面半径是2厘米,侧面积是12.56平方厘米,这个圆柱的体积是
如图,把一个圆柱体切拼成一个近似长方体,再把这个长方体侧放,你就会有一种巧妙的方法算出圆柱的体积.如果圆柱的底面半径是2厘米,侧面积是12.56平方厘米,这个圆柱的体积是 如图,把一个圆柱的底面平均切成16份,然后沿着高垂直把这个圆柱切开,拼成一个和它体积相等的近似长方体.测得这个长方体的宽是10厘米,高是25厘米.这个近似长方体的体积是
如图,把一个圆柱的底面平均切成16份,然后沿着高垂直把这个圆柱切开,拼成一个和它体积相等的近似长方体.测得这个长方体的宽是10厘米,高是25厘米.这个近似长方体的体积是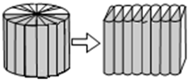 如图,把一个圆柱切拼成一个近似的长方体,这时长方体的表面积比原来增加了12平方厘米.如果截成两个小圆柱它的表面积增加了6.28平方厘米,求原来圆柱体的表面积________.
如图,把一个圆柱切拼成一个近似的长方体,这时长方体的表面积比原来增加了12平方厘米.如果截成两个小圆柱它的表面积增加了6.28平方厘米,求原来圆柱体的表面积________.