题目内容
 如图是6×6的方格纸,小方格纸的面积是1平方厘米,小方格的顶点称为格点.请你在图上选8个格点,要求其中任意3个格点都不在一条直线,并且使这8个点用直线连接后所围成的图形面积尽可能的大.
如图是6×6的方格纸,小方格纸的面积是1平方厘米,小方格的顶点称为格点.请你在图上选8个格点,要求其中任意3个格点都不在一条直线,并且使这8个点用直线连接后所围成的图形面积尽可能的大.(1)在图中划出所围成的图形;
(2)所围成图形的面积是
25
25
平方厘米.分析:(1)若使8个点连接后所围成的图形面积尽可能大,且其中任意3个格点都不在一条直线上,就要地每条边上取两个格点,且每两个格点的边线不能经过格点.
(2)根据毕克定理:格点面积=内部格点数+周界上格点数÷2-1.据此解答.
(2)根据毕克定理:格点面积=内部格点数+周界上格点数÷2-1.据此解答.
解答:解:(1)根据分析画图如下:
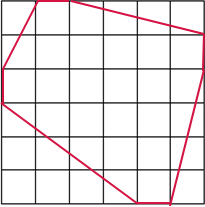
(2)22+8÷2-1,
=22+4-1,
=25(平方厘米).
答:所围成图形的面积是25平方厘米.
故答案为:25.

(2)22+8÷2-1,
=22+4-1,
=25(平方厘米).
答:所围成图形的面积是25平方厘米.
故答案为:25.
点评:本题考查了学生运用毕克定理解答问题的能力,本题的关键是周界上共8个格点,每两个格点的边线不经过第三格点.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 如图是6×6的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选8个格点,要求其中任意3个格点都不在一条直线上,并且使这8个点用直线连接后所围成的图形面积尽可能大.那么,所围图形的面积是
如图是6×6的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选8个格点,要求其中任意3个格点都不在一条直线上,并且使这8个点用直线连接后所围成的图形面积尽可能大.那么,所围图形的面积是 有一个3×3的方格纸,如图,甲、乙两人轮流往方格里填写1、3、4、5、6、7、8、9、10这九个数字,最后甲的得分是上、下两行6个数的和,乙的得分是左、右两列六个数的和,得分多的胜,请你为甲找出一种必胜的方法.
有一个3×3的方格纸,如图,甲、乙两人轮流往方格里填写1、3、4、5、6、7、8、9、10这九个数字,最后甲的得分是上、下两行6个数的和,乙的得分是左、右两列六个数的和,得分多的胜,请你为甲找出一种必胜的方法.