题目内容
如图的两个圆只有一个公共点A，大圆直径48厘米，小圆直径30厘米．两只甲虫同时从A点出发，按箭头所指的方向以相同速度分别沿两个圆爬行．当小圆上的甲虫爬了4
4
圈时，两只甲虫相距最远．分析：圆内的任意两点，以直径两端点的距离最远．如果沿小圆爬行的甲虫爬到A点，沿大圆爬行的甲虫恰好爬到B点，二甲虫的距离便最远．小圆周长为π×30=30π，大圆周长为48π，一半便是24π．问题便变为求30π和24π的“最小公倍数”问题了．
解答：解：30π和24π的最小倍数，相当于30与24的最小公倍数再乘以π．
30与24的最小公倍数是120，
120÷30=4，
120÷24=5．
所以小圆上甲虫爬4圈后，大圆上爬行了5个
圆周长，即是爬到了B点．
故答案为：4
30与24的最小公倍数是120，
120÷30=4，
120÷24=5．
所以小圆上甲虫爬4圈后，大圆上爬行了5个
| 1 |
| 2 |
故答案为：4
点评：此题主要考查圆周长公式，和求两个最小公倍数等知识．关键先理解圆内的任意两点，以直径两端点的距离最远．
练习册系列答案
相关题目
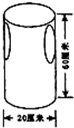某不锈钢五金加工厂计划生产一种圆柱体垃圾筒，为了节省材料，（如图）设计人员利用垃圾筒左右两侧开孔作垃圾入口．剪出的两个圆作垃圾筒的上、下两个底面．这样，①生产一个垃圾筒要用多少平方分米不锈钢板？（接口忽略不计） ②如果这个垃圾筒只有它容积的70%可以装垃圾，那么，装垃圾部分的容积是多少立方分米？（钢板厚度忽略不计，得数保留一位小数）
如图圆上的A点为圆心画一个圆，使这两个圆组成的新图形只有两条对称轴．画出这两条对称轴．
如图，两个圆周只有一个公共点A，大圆直径AB为48厘米，小圆直径AC为30厘米，甲、乙两虫同时从A点出发，甲虫以每秒0.5厘米的速度顺时针沿大圆圆周爬行，乙虫以同样速度顺时针沿小圆圆周爬行．（本题π=3）
如图，两个圆周只有一个公共点A，大圆直径AB为48厘米，小圆直径AC为30厘米，甲、乙两虫同时从A点出发，甲虫以每秒0.5厘米的速度顺时针沿大圆圆周爬行，乙虫以同样速度顺时针沿小圆圆周爬行．（本题π=3）