题目内容
（2012?北京模拟）（1）如图，将4块棱长为1的正方体木块排成一排，拼成一个长方体．那么拼合后这个长方体的表面积，比原来4个正方体的表面积之和少了多少？
（2）一个正方体形状的木块，棱长为1，如图所示，将其切成两个长方体，这两部分的表面积总和是多少？如果在此基础上再切4刀，将其切成大大小小共18块长方体．这18块长方体表面积总和又是多少？
（2）一个正方体形状的木块，棱长为1，如图所示，将其切成两个长方体，这两部分的表面积总和是多少？如果在此基础上再切4刀，将其切成大大小小共18块长方体．这18块长方体表面积总和又是多少？
分析：（1）观察图形可知，拼组后的长方体的表面积比原来减少了6个小正方体的面的面积，由此即可解答；
（2）每切一刀，就增加2个正方体的面，所以这两部分的表面积之和就是8个正方体的面的面积之和；在此基础上再切4刀后，表面积比原来又增加了8个小正方体的面，由此即可解答．
（2）每切一刀，就增加2个正方体的面，所以这两部分的表面积之和就是8个正方体的面的面积之和；在此基础上再切4刀后，表面积比原来又增加了8个小正方体的面，由此即可解答．
解答：解：（1）6×1×1=6，
答：拼组后表面积减少了6．
（2）切一刀，得到的两个长方体的表面积之和是：1×1×（6+2）=8；
再切4刀，则表面积之和是：1×1×（6+10）=16；
答：切一刀后，表面积之和是8，再切4刀后，表面积之和是16．
答：拼组后表面积减少了6．
（2）切一刀，得到的两个长方体的表面积之和是：1×1×（6+2）=8；
再切4刀，则表面积之和是：1×1×（6+10）=16；
答：切一刀后，表面积之和是8，再切4刀后，表面积之和是16．
点评：抓住正方体的切割特点，得出每切1刀增加的表面积规律，是解决此类问题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
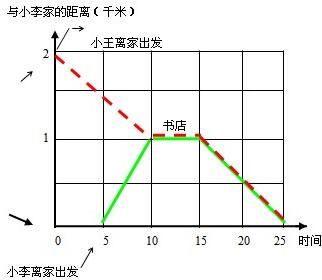（2012?北京模拟）下面是小王和小李外出情况的一张折线统计图．他们分别住在一条大街的两头，相距2千米，在他们两家之间，中途恰好是一所书店．现在请根据下图，回答问题：