题目内容
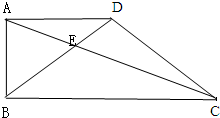 (2011?长春模拟)如图,在直角梯形ABCD中,上底AD的长是12厘米,高AB长9厘米,BE=2ED,底边BC长多少厘米?
(2011?长春模拟)如图,在直角梯形ABCD中,上底AD的长是12厘米,高AB长9厘米,BE=2ED,底边BC长多少厘米?分析:由图知:△ABE与△ADE等高,而两个△的底边都在BD上,因为BE=2ED,所以S△ABE=2S△ADE;又因为△CBE与△CDE等高,而这两个△的底边也共在BD上,同样可求S△CBE=2S△CDE,又因为△ABE+△CBE=△ABC,△ADE+△CDE=△DCA,所以S△ABC═2S△DCA,又因为△ABC与△DAC等高,所以△ABC的底BC是△DAC的底AD的2倍,所以BC=2×AD=2×12=24(厘米).
解答:解:由图知:△ABE与△ADE等高,△ABE的底是BE,△ADE的底是ED,
因为BE=2ED,所以S△ABE=2S△ADE;
又因为△CBE与△CDE等高,△CBE的底是BE,△CDE的底是ED,BE=2ED,
所以S△CBE=2S△CDE,
又因为△ABE+△CBE=△ABC,△ADE+△CDE=△DCA,
所以S△ABC=2(S△ADE+S△CDE)=2S△DCA,
又因为△ABC与△DAC等高,
所以△ABC的底BC是△DAC的底AD的2倍,
又因为AD=12(厘米),
所以BC=2×12=24(厘米).
因为BE=2ED,所以S△ABE=2S△ADE;
又因为△CBE与△CDE等高,△CBE的底是BE,△CDE的底是ED,BE=2ED,
所以S△CBE=2S△CDE,
又因为△ABE+△CBE=△ABC,△ADE+△CDE=△DCA,
所以S△ABC=2(S△ADE+S△CDE)=2S△DCA,
又因为△ABC与△DAC等高,
所以△ABC的底BC是△DAC的底AD的2倍,
又因为AD=12(厘米),
所以BC=2×12=24(厘米).
点评:此题关键在于找同高的三角形,反正两方面利用两个三角形高相同的情况下底边与面积的对应关系.

练习册系列答案
相关题目
