题目内容
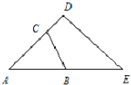 如图,已知△ABC面积为2,D为AC延长线上一点,且AC=2CD,E为AB延长线上一点,且BE=AB,求△ADE的面积.
如图,已知△ABC面积为2,D为AC延长线上一点,且AC=2CD,E为AB延长线上一点,且BE=AB,求△ADE的面积.分析:连接BD,则三角形ADB和三角形DBE是等底等高的三角形,则其面积相等;而三角形ABC与三角形DBC是等高不等底的三角形,则其面积比就等于对应底的比,再据“且AC=2CD”可知,三角形ABC的面积是三角形DBC面积的2倍,从而逐步求得三角形ADE的面积.
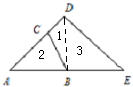
解答:解:如图,连接BD,设△BCD的面积为1份,则△ABC的面积为2份,△BDE的面积为3份;
所以△ABC的面积是△ADE的
=
,
2÷
=6;
答:△ADE的面积是6.
所以△ABC的面积是△ADE的
| 2 |
| 1+2+3 |
| 1 |
| 3 |
2÷
| 1 |
| 3 |
答:△ADE的面积是6.

点评:解答此题的主要依据是:等底等高的三角形面积相等,等高不等底的三角形面积比就等于对应底的比.

练习册系列答案
相关题目
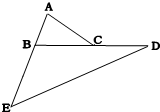 如图,已知△ABC的面积为1平方米.BE=2AB,BC=CD,求三角形BDE的面积.
如图,已知△ABC的面积为1平方米.BE=2AB,BC=CD,求三角形BDE的面积.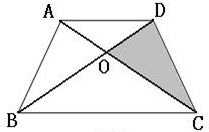 如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积?
如图,已知四边形ABCD为梯形,AD=2厘米、BC=5厘米,且三角形ABC的面积为5平方厘米,求阴影部分面积? 如图,已知ABC为扇形,BDF为扇形,CBDE为长方形.CE=8厘米,CB=10厘米求图中阴影部分的面积.
如图,已知ABC为扇形,BDF为扇形,CBDE为长方形.CE=8厘米,CB=10厘米求图中阴影部分的面积.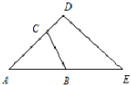 如图,已知△ABC面积为2,D为AC延长线上一点,且AC=2CD,E为AB延长线上一点,且BE=AB,求△ADE的面积.
如图,已知△ABC面积为2,D为AC延长线上一点,且AC=2CD,E为AB延长线上一点,且BE=AB,求△ADE的面积.