题目内容
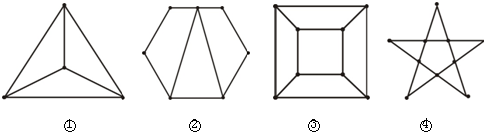
如图,①②③④四个图都称作平面图,观察图①和表中对应数值,探究计数的方法并作答.
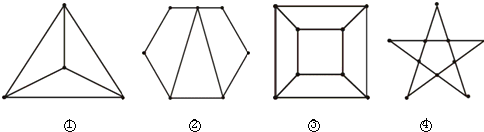
(1)数一数,每个图各有多少个顶点,多少条边,这些边围出多少区域,并将结果填入下表:
| 图 | ① | ② | ③ | ④ |
| 顶点数m | 4 | 7 | ||
| 边数n | 6 | 9 | ||
| 区域数f | 3 |
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系,则这个平面有________条边.
解:填表如下:
(2)平面图的定点数m、边数n、区域数f之间的一种关系:n=m+f-1;
(3)这个平面有:20+11-1=30(条).
故答案为:n=m+f-1;30.
分析:(1)由所给的b图表格数据得出:
①图顶点数为4个,6条边,围成3个区域;
②图有7个顶点,9条边,围成3个区域;
③图有8个顶点,12条边,围成5个区域;
d图有10个顶点,15条边,围成6个区域;
(2)根据表中数值得出平面图形的顶点数、边数、区域数之间的关系为:顶点数+区域数-1=边数;
(3)将数据代入(2)的公式计算即可.
点评:此题主要考查了计数方法的应用,根据四个不同的图形分别列举得出规律是解题的关键.
| 图 | ① | ② | ③ | ④ |
| 顶点数m | 4 | 7 | 8 | 10 |
| 边数n | 6 | 9 | 12 | 15 |
| 区域数f | 3 | 3 | 5 | 6 |
(3)这个平面有:20+11-1=30(条).
故答案为:n=m+f-1;30.
分析:(1)由所给的b图表格数据得出:
①图顶点数为4个,6条边,围成3个区域;
②图有7个顶点,9条边,围成3个区域;
③图有8个顶点,12条边,围成5个区域;
d图有10个顶点,15条边,围成6个区域;
(2)根据表中数值得出平面图形的顶点数、边数、区域数之间的关系为:顶点数+区域数-1=边数;
(3)将数据代入(2)的公式计算即可.
点评:此题主要考查了计数方法的应用,根据四个不同的图形分别列举得出规律是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 如图,用四个完全相同的直角三角形可以拼成一个中间空心的正方形.如果这个正方形的边长是15厘米,中间空心的小正方形的边长是3厘米,直角三角形长的直角边是12厘米,那么短的那条直角边是多少厘米?你还能用这四个直角三角形拼出正方形吗?
如图,用四个完全相同的直角三角形可以拼成一个中间空心的正方形.如果这个正方形的边长是15厘米,中间空心的小正方形的边长是3厘米,直角三角形长的直角边是12厘米,那么短的那条直角边是多少厘米?你还能用这四个直角三角形拼出正方形吗? (2011?北海模拟)一块长方形铁板,长30厘米,宽25厘米.像如图那样从四个角切掉边长为5厘米的正方形,然后做成盒子.这个盒子的容积有多少毫升?
(2011?北海模拟)一块长方形铁板,长30厘米,宽25厘米.像如图那样从四个角切掉边长为5厘米的正方形,然后做成盒子.这个盒子的容积有多少毫升?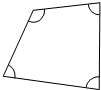 量出如图四边形的四个角,标在图上;这四个角的总和是
量出如图四边形的四个角,标在图上;这四个角的总和是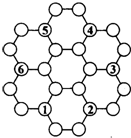 如图,有六个正六边形和二十四个小圆圈,l-6已填人圆圈内,将100-117填人圆圈内,使每个正六边形六个圆圈内的数字之和都是a,则这个a是
如图,有六个正六边形和二十四个小圆圈,l-6已填人圆圈内,将100-117填人圆圈内,使每个正六边形六个圆圈内的数字之和都是a,则这个a是