题目内容
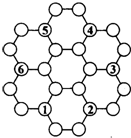如图，有六个正六边形和二十四个小圆圈，l-6已填人圆圈内，将100-117填人圆圈内，使每个正六边形六个圆圈内的数字之和都是a，则这个a是435
435
．分析：因为要a的值最小，所以把最小的六个数100、101、102、103、104、105填入最里面的六个圆圈，其余的12个数填入外面的圆圈，再根据最外面的12个数都用一次，其余的12个数都用两次，然后求出总和再除以6就是最小的a值．
解答：解：因为要填入的数里面的被用两次，外面的被用一次，
所以要使a值最小，须把最小的六个数填入，里面的六个圆圈，
因为六个正六边形的数字总和为：
（1+2+…+6+100+101+…+105）×2+（106+107+…+117）
=（21+615）×2+（106+117）×12÷2，
=1272+1338，
=2610．
所以a=2610÷6=435．
故答案为：435．
所以要使a值最小，须把最小的六个数填入，里面的六个圆圈，
因为六个正六边形的数字总和为：
（1+2+…+6+100+101+…+105）×2+（106+107+…+117）
=（21+615）×2+（106+117）×12÷2，
=1272+1338，
=2610．
所以a=2610÷6=435．
故答案为：435．
点评：确定里面圆圈填入的数字是解题的关键，也是本题的突破口，有一定的难度且有技巧性．．
练习册系列答案
相关题目
如图，正方体的棱长为6cm，连接正方体其中六条棱的中点形成一个正六边形，而连接其中三个顶点形成一个三角形．正方体夹在六边形与三角形之间的立体图形有