题目内容
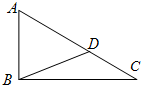 如图,直角三角形ABC中,∠ABC=90°,∠ACB=30°,点D在AC上,如果∠ADB=45°,那么∠ABD=
如图,直角三角形ABC中,∠ABC=90°,∠ACB=30°,点D在AC上,如果∠ADB=45°,那么∠ABD=75
75
度.分析:依据三角形的内角和是180度,因为,∠ABC=90°,∠ACB=30°,则可以求出∠BAD=180°-90°-30°,又因∠ADB=45°,进而就可以求出∠ABD的度数.
解答:解:因为,∠ABC=90°,∠ACB=30°,
则∠BAD=180°-90°-30°=60°,
又因∠ADB=45°,
所以∠ABD=180°-45°-60°=75°;
故答案为:75.
则∠BAD=180°-90°-30°=60°,
又因∠ADB=45°,
所以∠ABD=180°-45°-60°=75°;
故答案为:75.
点评:此题主要考查三角形的内角和定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图:直角三角形ABC中,AB=6分米,BC=4分米,如果以AB为轴旋转一周,可得到一个什么形体,这个形体的体积是多少?
如图:直角三角形ABC中,AB=6分米,BC=4分米,如果以AB为轴旋转一周,可得到一个什么形体,这个形体的体积是多少? (2011?广州模拟)如图,直角三角形ABC中,AB是圆的直径,且AB=20厘米,如果阴影a的面积比阴影b的面积大7平方厘米,BC的长度是
(2011?广州模拟)如图,直角三角形ABC中,AB是圆的直径,且AB=20厘米,如果阴影a的面积比阴影b的面积大7平方厘米,BC的长度是 (2007?江阴市)如图将直角三角形以直角边AB为轴旋转一周,所得的立体图形的体积是
(2007?江阴市)如图将直角三角形以直角边AB为轴旋转一周,所得的立体图形的体积是 (2004?武汉)如图,直角三角形的三边为3,4,5,EF,EG,ED垂直于AB,BC,CA,且EF=EG=ED,求EF.
(2004?武汉)如图,直角三角形的三边为3,4,5,EF,EG,ED垂直于AB,BC,CA,且EF=EG=ED,求EF. 如图:直角三角形ABC,AC=4厘米,AB=5厘米,BC=3厘米,如果以AC边旋转一周的空间是
如图:直角三角形ABC,AC=4厘米,AB=5厘米,BC=3厘米,如果以AC边旋转一周的空间是