题目内容
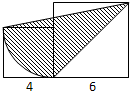 图中给出了两个对齐摆放的正方形,并以小正方形中右上顶点为圆心,边长为半径作一个扇形,按图中所给长度阴影部分面积为
图中给出了两个对齐摆放的正方形,并以小正方形中右上顶点为圆心,边长为半径作一个扇形,按图中所给长度阴影部分面积为28.56
28.56
.(π=3.14)分析:给图中各点加上字母如下图所示:
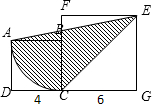
连接AC后如下图:
根据S阴=S△ACD+S扇-SABC,求解即可.

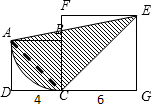
连接AC后如下图:

根据S阴=S△ACD+S扇-SABC,求解即可.
解答:解:连接AC后如下图:

S阴=S△ACD+S扇-SABC,
因为
×
AC2=
×4×4,
所以AC2=32,
同理CE2=72,所以AC×CE=48,
所以S△ACD=
×48=24,
S扇=
πr2,
=
×3.14×42,
=12.56,
SABC=
×4×4=8,
所以S阴=24+12.56-8=28.56,
故答案为:28.56.

S阴=S△ACD+S扇-SABC,
因为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以AC2=32,
同理CE2=72,所以AC×CE=48,
所以S△ACD=
| 1 |
| 2 |
S扇=
| 90 |
| 360 |
=
| 1 |
| 4 |
=12.56,
SABC=
| 1 |
| 2 |
所以S阴=24+12.56-8=28.56,
故答案为:28.56.
点评:此题的关键是给两个正方形标上字母后,连接AC,从而根据S阴=S△ACD+S扇-SABC求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
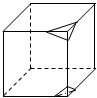 如图,立方体的每个角被切下去(图中仅画了两个),问得到的几何体有多少个棱?
如图,立方体的每个角被切下去(图中仅画了两个),问得到的几何体有多少个棱?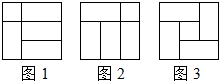 图中给出了三种方法将一个3×3的正方形分成一个1×1的正方形和四个2×1的长方形,那么将一个3×3的正方形分成一个1×1的正方形和四个2×1的长方形,一共有( )种方法.
图中给出了三种方法将一个3×3的正方形分成一个1×1的正方形和四个2×1的长方形,那么将一个3×3的正方形分成一个1×1的正方形和四个2×1的长方形,一共有( )种方法.
 图中给出了两个对齐摆放的正方形,并以小正方形中右上顶点为圆心,边长为半径作一个扇形,按图中所给长度阴影部分面积为________.(π=3.14)
图中给出了两个对齐摆放的正方形,并以小正方形中右上顶点为圆心,边长为半径作一个扇形,按图中所给长度阴影部分面积为________.(π=3.14)