题目内容
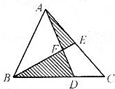如图，在△ABC中，BD：DC=2：1，E是AC边的中点，AD与BE相交于F点．如果△ABC的面积是60平方厘米，求图中阴影部分的面积．分析：连接GC，由图意可以看出，S△FBD=2S△FDC，S△AFE=S△EFC，S△ADE=S△BEC，从而可以推出结果．
解答：解：如图，连接FC
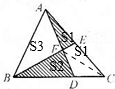
S△FBD=2S△FDC=S2，
S△AFB=S3
S△AEF=S△EFC=S1
S△AEB=S△BEC=S1+S3=S1+
+S2=60÷2=30（平方厘米），
所以S1+S3=30（平方厘米）；且S3=3
；
S△ABD=2S△ADC得，
S3+S2=2（S1+S1+
）=40（平方厘米），
得 S2=16（平方厘米），
S1=6（平方厘米），
则阴影的面积是16+6=22（平方厘米）；
答：阴影部分的面积是22平方厘米．
S△FBD=2S△FDC=S2，
S△AFB=S3
S△AEF=S△EFC=S1
S△AEB=S△BEC=S1+S3=S1+
| S2 |
| 2 |
所以S1+S3=30（平方厘米）；且S3=3
| S2 |
| 2 |
S△ABD=2S△ADC得，
S3+S2=2（S1+S1+
| S2 |
| 2 |
得 S2=16（平方厘米），
S1=6（平方厘米），
则阴影的面积是16+6=22（平方厘米）；
答：阴影部分的面积是22平方厘米．
点评：此题主要考查图形面积间的等积代换．
练习册系列答案
相关题目
如图，在△ABC中，D为BC边上任一点，AE=
如图，在△ABC中，两条角平分线CD、EF相交于F，∠A=60°，则∠DFE=
（2013?北京模拟）如图，在△ABC中，AD=
如图，在△ABC中，E、D、F分别为AD、BC、AB的中点，BD=DE=EC，BF=FA，△EDF的面积是1，那么△ABC的面积是多少？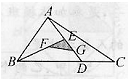
如图，在△ABC中，