题目内容
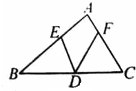 如图,在三角形ABC中,角A=80度,BD=BE,CD=CF,则角EDF=________度?
如图,在三角形ABC中,角A=80度,BD=BE,CD=CF,则角EDF=________度?
50
分析:要求∠EDF的度数,由平角的定义可知,只要求出∠BDE+∠CDF即可解决问题.根据三角形内角和是180°和等腰三角形的两个底角相等即可解决问题.
解答:在△ABC中利用三角形的内角和是180°可得∠B+∠C=180°-80°=100°
在△BDE中,因为BD=BE,所以∠BDE= ×(180°-∠B)=90°-
×(180°-∠B)=90°- ∠B;
∠B;
同样可得,∠CDF=90°- ∠C,
∠C,
所以∠BDE+∠CDF=90°- ∠B+90°-
∠B+90°- ∠C=180°-
∠C=180°- ×(∠B+∠C)=180°-
×(∠B+∠C)=180°- ×100°=130°;
×100°=130°;
所以∠EDF=180°-130°=50°,
答:∠EDF=50°.
故答案为:50.
点评:转化思想在数学学习中尤为重要,要求∠EDF的度数可以转化为求∠BDE+∠CDF得度数和,利用三角形的内角和及等腰三角形的性质即可解决问题.
分析:要求∠EDF的度数,由平角的定义可知,只要求出∠BDE+∠CDF即可解决问题.根据三角形内角和是180°和等腰三角形的两个底角相等即可解决问题.
解答:在△ABC中利用三角形的内角和是180°可得∠B+∠C=180°-80°=100°
在△BDE中,因为BD=BE,所以∠BDE=
 ×(180°-∠B)=90°-
×(180°-∠B)=90°- ∠B;
∠B;同样可得,∠CDF=90°-
 ∠C,
∠C,所以∠BDE+∠CDF=90°-
 ∠B+90°-
∠B+90°- ∠C=180°-
∠C=180°- ×(∠B+∠C)=180°-
×(∠B+∠C)=180°- ×100°=130°;
×100°=130°;所以∠EDF=180°-130°=50°,
答:∠EDF=50°.
故答案为:50.
点评:转化思想在数学学习中尤为重要,要求∠EDF的度数可以转化为求∠BDE+∠CDF得度数和,利用三角形的内角和及等腰三角形的性质即可解决问题.

练习册系列答案
相关题目
 如图,在三角形ABC中,BD:DC=1:2,AE=ED,则AF:FC=( )
如图,在三角形ABC中,BD:DC=1:2,AE=ED,则AF:FC=( ) 如图:在三角形ABC中,BD=
如图:在三角形ABC中,BD= 如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的( ) 倍.
如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的( ) 倍. 如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的
如图,在三角形ABC中,CD的长是BD长的2倍,E是AC的中点,则三角形ABC的面积是三角形ADE面积的 如图,在三角形ABC中,D、E为两个三等分点,F为AB的中点,若△EDF的面积是12平方厘米,则△ABC的面积是( )平方厘米.
如图,在三角形ABC中,D、E为两个三等分点,F为AB的中点,若△EDF的面积是12平方厘米,则△ABC的面积是( )平方厘米.