题目内容
15．在15、17、18、15、18、19、18、19、20、21中，中位数是18，平均数是18众数是18．分析 将数据按照从小到大或从大到小的顺序排列，如果数据个数是奇数，则处于最中间位置的数就是这组数据的中位数；如果数据的个数是偶数，则中间两个数据的平均数是这组数据的中位数；把给出的这7个数据加起来再除以数据个数7，就是此组数据的平均数；在此组数据中出现次数最多的那个数，就是此组数据的众数．解答即可．
解答 解：将15、17、18、15、18、19、18、19、20、21按从小到大的顺序排列为：
15、15、17、18、18、18、19、19、20、21；
（18+18）÷2=18
所以这组数据的中位数是18．
这组数据中出现次数最多的数是18，
所以18是这组数据的众数；
平均数：（15+17+18+15+18+19+18+19+20+21）÷10
=180÷10
=18
故答案为：18、18、18．
点评 此题主要考查了平均数、中位数与众数的意义与求解方法．
练习册系列答案
相关题目
20．计算下面各题，能用简便算法的用简便算法
| $\frac{5}{9}$+$\frac{8}{15}$+$\frac{1}{15}$+$\frac{4}{9}$ | $\frac{5}{12}$+$\frac{7}{8}$+$\frac{7}{12}$ | $\frac{13}{25}$-$\frac{13}{50}$+$\frac{1}{5}$ |
| 7-（$\frac{3}{4}$-$\frac{2}{5}$） | $\frac{2}{3}$-$\frac{2}{9}$+$\frac{1}{3}$-$\frac{7}{9}$ | $\frac{3}{4}$-（$\frac{1}{2}$+$\frac{1}{4}$） |
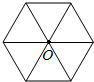，如绕点O最少旋转60度后与原来的图形重合．