题目内容
如图，三角形ABC中，AB=AC，AE=AD，∠BAD=30°．∠ACD=40°，那么，∠EDC=
15
15
度．分析：要求∠EDC，在△EDC中，只要求出∠DEC即可；要求出∠DEC，只要求出∠AED即可，在△ADE中，AD=AE，只要求出∠DAE即可解决；在△ABC中可以求出∠BAC的度数，由此可以解决问题．
解答：解：在△ABC中，AB=AC，∠C=40°，所以∠BAC=180°-40°×2=100°；
∠DAE=100°-30°=70°，
在△ADE中，AD=AE，所以∠AED（=180°-70°）÷2=55°，
所以∠DEC=180°-55°=125°（平角的定义），
所以在△EDC中，∠EDC=180°-40°-125°=15°，
故答案为：15．
∠DAE=100°-30°=70°，
在△ADE中，AD=AE，所以∠AED（=180°-70°）÷2=55°，
所以∠DEC=180°-55°=125°（平角的定义），
所以在△EDC中，∠EDC=180°-40°-125°=15°，
故答案为：15．
点评：运用逆向思维对要求的问题进行分析，此题步步紧扣等腰三角形的性质和三角形的内角和进行推理解答．
练习册系列答案
相关题目
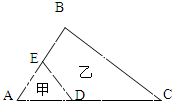（2012?德江县模拟）如图的三角形ABC中，AD：DC=2：3，AE=EB． 甲乙两个图形面积的比是（ ）
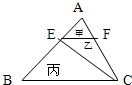如图，三角形ABC中，EF平行于BC，AB=4AE，三角形甲、乙、丙的面积之比是
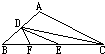如图在三角形ABC中，D点为AB的中点，E点为BC的中点，F点为BE的中点，已知三角形DCF面积为63平方厘米，则三角形ABC面积为多少平方厘米？
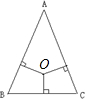如图，三角形ABC中有一点O，O点到三条边的垂线段长都是3厘米．又知道三角形的周长是30厘米，那么三角形ABC的面积是