题目内容
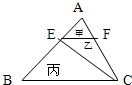 如图,三角形ABC中,EF平行于BC,AB=4AE,三角形甲、乙、丙的面积之比是
如图,三角形ABC中,EF平行于BC,AB=4AE,三角形甲、乙、丙的面积之比是1:3:12
1:3:12
.分析:由“EF平行于BC,AB=4AE”可得:AE:AB=1:4,AF:AC=1:4,再据“等高不等底的三角形的面积比就等于其对应底的比”,所以甲=
S△AEC,乙=
S△AEC,丙=
S△ABC,又因S△AEC=
S△ABC,于是就可以求出三角形甲、乙、丙的面积之比.
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
解答:解:因为AE:AB=1:4,AF:AC=1:4,
所以甲=
S△AEC,乙=
S△AEC,丙=
S△ABC,
又因S△AEC=
S△ABC,
则甲=
S△AEC,
=
×
S△ABC,
=
S△ABC,
乙=
S△AEC,
=
×
S△ABC,
=
S△ABC,
所以S甲:S乙:S丙=
:
:
=1:3:12;
故答案为:1:3:12.
所以甲=
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
又因S△AEC=
| 1 |
| 4 |
则甲=
| 1 |
| 4 |
=
| 1 |
| 4 |
| 1 |
| 4 |
=
| 1 |
| 16 |
乙=
| 3 |
| 4 |
=
| 3 |
| 4 |
| 1 |
| 4 |
=
| 3 |
| 16 |
所以S甲:S乙:S丙=
| 1 |
| 16 |
| 3 |
| 16 |
| 3 |
| 4 |
故答案为:1:3:12.
点评:解答此题的主要依据是:等高不等底的三角形的面积比就等于其对应底的比.

练习册系列答案
相关题目
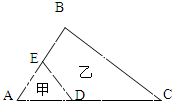 (2012?德江县模拟)如图的三角形ABC中,AD:DC=2:3,AE=EB. 甲乙两个图形面积的比是( )
(2012?德江县模拟)如图的三角形ABC中,AD:DC=2:3,AE=EB. 甲乙两个图形面积的比是( )
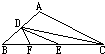 如图在三角形ABC中,D点为AB的中点,E点为BC的中点,F点为BE的中点,已知三角形DCF面积为63平方厘米,则三角形ABC面积为多少平方厘米?
如图在三角形ABC中,D点为AB的中点,E点为BC的中点,F点为BE的中点,已知三角形DCF面积为63平方厘米,则三角形ABC面积为多少平方厘米?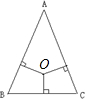 如图,三角形ABC中有一点O,O点到三条边的垂线段长都是3厘米.又知道三角形的周长是30厘米,那么三角形ABC的面积是
如图,三角形ABC中有一点O,O点到三条边的垂线段长都是3厘米.又知道三角形的周长是30厘米,那么三角形ABC的面积是