题目内容
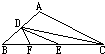如图在三角形ABC中，D点为AB的中点，E点为BC的中点，F点为BE的中点，已知三角形DCF面积为63平方厘米，则三角形ABC面积为多少平方厘米？分析：由“D点为AB的中点，E点为BC的中点，F点为BE的中点”可得：S△DCF=
S△DCB，S△DCB=
S△ABC，S△DCF=
S△ABC，于是利用分数除法的意义，即可求出三角形ABC的面积．
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
解答：解：据分析可知：S△DCF=
S△DCB，S△DCB=
S△ABC，S△DCF=
S△ABC，
所以三角形ABC的面积为：63÷
=168（平方厘米），
答：三角形ABC面积为168平方厘米．
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
所以三角形ABC的面积为：63÷
| 3 |
| 8 |
答：三角形ABC面积为168平方厘米．
点评：解答此题的主要依据是：等高不等底的三角形的面积比就等于对应底的比．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
如图直角三角形ABC中，已知AB=21厘米，BC=28厘米，如果在这个直角三角形中作一个尽量大的正方形，那么这个正方形的面积是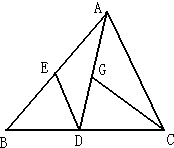
如图，在三角形ABC中，E、D、G分别是AB、BC、AD的中点，图中与三角形ADE面积相等的三角形还有（ ）
在三角形ABC中，一个锐角是30°．截去这个角后（如图），剩下图形的内角和是多少度？
如图，在三角形ABC中，CD的长是BD长的2倍，E是AC的中点，则三角形ABC的面积是三角形ADE面积的