题目内容
【题目】宝强开车从A城市到B城市，从开始出发，车速即比原计划的速度提高了
，结果提前1.5小时到达；返回时，按原计划的速度行驶280千米后，将车速提高
，于是提前1小时40分钟到达A城市．求A、B两座城市之间的路程．
【答案】1260千米
【解析】
把原计划的车速看作单位“1”，提高
的的速度是（1+），用原计划的车速除以提高后的车速，求出原计划车速是提高后车速的几分之几；根据分数除法的意义，求出原来速度行驶下所需要的时间；再求出后来的速度是最后速度的几分之几，进而求出后来所用的时间；然后根据分数除法的意义，求出原来的速度，再依据路程、速度、时间三者之间的关系求出A、B两地的距离
1小时40分＝
小时
原来的速度相当于提速后的：
1÷（1+）
＝1÷
＝
原来时间：
1.5÷（1﹣）
＝1.5÷
＝15（小时）
原车速相当于提高
后车速的：
1÷（1+）
＝1÷
＝
最后的用的时间：
÷（1﹣）
＝÷
＝
原来的车速：
280÷（15﹣）
＝280÷
＝84（千米）
84×15＝1260（千米）
答：A、B两座城市之间的路程是1260千米．
练习册系列答案
灵星计算小达人系列答案
相关题目
【题目】根据表中的数据，在下图中描出相应的点，并把它们用线连起来
路程/千米 | 时间/时 |
30 | 1 |
60 | 2 |
90 | 3 |
120 | 4 |
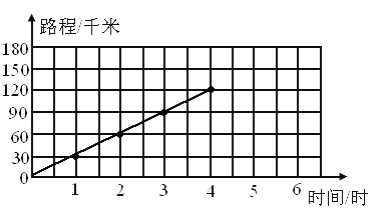
（1）路程和时间成比例吗？________(填成或不成)成什么比例？________(填正比例、反比例或不成比例)
（2）根据图像判断，这辆汽车行驶150千米需要________小时？6小时能行驶________千米？
（3）根据表格中的数据，在图中描出相应的点，并把它们用线连起来.
