题目内容
如图，三角形ABC是等边三角形，D、E分别是AB和AC的中点．三角ADE面积是梯形BDEC面积的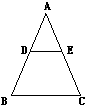
- A.
- B.
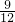
- C.
C
分析：三角形ABC是等边三角形，D、E分别是AB和AC的中点，则BC=2DE，三角形ADE的高等于梯形BDEC的高，设它们的高为h，设BC为4，则DE为2，运用公式分别求出三角形与梯形的面积，二者相除得到答案后选择即可．
解答：设三角形ADE与梯形BDEC的高为h，设BC为4，则DE为2，
三角形ADE的面积：2×h÷2=h；
梯形BDEC的面积：（4+2）×h÷2=6h÷2=3h，
三角ADE面积是梯形BDEC面积的：h÷3h=；
故选：C．
点评：此题关键是明白连接等边三角形的中点的线段，长度是等边三角形边的一半，据此解决问题．
分析：三角形ABC是等边三角形，D、E分别是AB和AC的中点，则BC=2DE，三角形ADE的高等于梯形BDEC的高，设它们的高为h，设BC为4，则DE为2，运用公式分别求出三角形与梯形的面积，二者相除得到答案后选择即可．
解答：设三角形ADE与梯形BDEC的高为h，设BC为4，则DE为2，
三角形ADE的面积：2×h÷2=h；
梯形BDEC的面积：（4+2）×h÷2=6h÷2=3h，
三角ADE面积是梯形BDEC面积的：h÷3h=
；故选：C．
点评：此题关键是明白连接等边三角形的中点的线段，长度是等边三角形边的一半，据此解决问题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
如图：三角形ABC是直角三角形，AC是圆的半径且AC=10cm．阴影Y的面积比阴影X的面积小32平方厘米．求BD的长．
（2012?中山市模拟）如图，三角形ABC是面积为46.8平方厘米的等边三角形，ABCD是平行四边形，圆的半径是6厘米，求阴影部分的面积．
（2012?福州）如图：三角形ABC是等腰直角三角形，直角边为4厘米，求阴影部分面积．
如图，三角形ABC是一个等腰三角形，AC=BC，已知∠ACD=130°，