Question

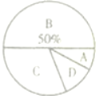
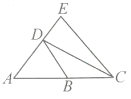
【题目】图中AB：BC=1：1，AD：DE=2：1，则△ABD与△ACE的面积比是________。（填最简整数比）

Answer 1

【答案】1:3

【解析】

三角形的面积=底×高÷2，因为AB：BC=1：1，观察图可知，△ABD和△BDC高相等，所以它们的面积也相等，又因为AD：DE=2：1，△ACD和△DCE的高相等，则S△ACD：S△DCE=2：1，因为S△ACD=S△ABD+S△BCD，S△ACE=S△ACD+S△DCE，由此可以求出△ABD与△ACE的面积比，据此列式解答。

因为AB：BC=1：1，所以S△ABD：S△BCD=1：1，又因为AD：DE=2：1，所以S△ACD：S△DCE=2：1，因为S△ACD=S△ABD+S△BCD ， S△ACE=S△ACD+S△DCE ， 所以S△ABD：S△ACE=1：3。

故答案为：1：3。