题目内容
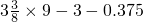
999×222+333×334
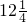 -(
-(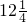 -(
-(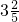 +2.25-3.6)
+2.25-3.6)
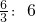 =
=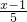
x- -
-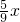 =
=
已知a=8.8+8.98+8.998+8.9998+8.99998,求a的整数部分.
解:(1)3 ×9-3-0.375,
×9-3-0.375,
=(3+0.375)×9-3-0.375,
=3×9+0.375×9-3-0.375,
=27-3+(9-1)×0.375,
=24+8× ,
,
=24+3,
=27;
(2)999×222+333×334,
=333×3×222+333×334,
=333×(666+334),
=333×1000,
=333000;
(3)12 -[12
-[12 -(3
-(3 +2.25-3.6)],
+2.25-3.6)],
=12 -12
-12 +(3
+(3 +2.25-3.6),
+2.25-3.6),
=3.4+2.25-3.6,
=2.05;
(4)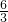 :6=
:6=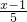 ,
,
1:3=(x-1):5,
3×(x-1)=5,
3x-3=5,
3x-3+3=5+3,
3x=8,
3x÷3=8÷3,
x= ;
;
(5)x- -
-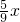 =
= ,
,
x(1- )-
)- =
= ,
,
x(1- )-
)- +
+ =
= +
+ ,
,
 x=
x= ,
,
 x×
x× =
= ×
× ,
,
x= ;
;
(6)a=8.8+8.98+8.998+8.9998+8.99998,
=(9-0.2)+(9-0.02)+(9-0.002)+(9-0.0002)+(9-0.00002),
=9×5-0.22222,
=45-0.22222,
=44.77778,
所以a的整数部分是44.
分析:(1)把3 拆成3+
拆成3+ ,并把
,并把 化为小数,运用乘法分配律的逆运算简算;
化为小数,运用乘法分配律的逆运算简算;
(2)观察可知,999是333的倍数,入江999×222转化为333×3×222,就可根据乘法分配律求出结果;
(3)根据数字特点,先去中括号,变为12 -12
-12 +(3
+(3 +2.25-3.6),再把3
+2.25-3.6),再把3 化为小数,计算即可;
化为小数,计算即可;
(4)先化简等式左边,原式变为1:3=(x-1):6,根据比例的基本性质改写成3×(x-1)=6,即3x-3=6,再根据等式的性质,两边同加上3,再同除以3即可;
(5)运用运算定律写成x(1- )-
)- =
= ,再根据等式的性质,两边同加
,再根据等式的性质,两边同加 ,得
,得 x=
x= ,两边再同乘
,两边再同乘 即可;
即可;
(6)此算式中的数字很有特点,把每个数看作9减去小数的形式,通过计算即可得出.
点评:查了简便运算与解方程等题目,灵活运用所学的运算定律以及数与数之间的联系进行简便计算,在解方程时,注意依据等式的性质.
 ×9-3-0.375,
×9-3-0.375,=(3+0.375)×9-3-0.375,
=3×9+0.375×9-3-0.375,
=27-3+(9-1)×0.375,
=24+8×
 ,
,=24+3,
=27;
(2)999×222+333×334,
=333×3×222+333×334,
=333×(666+334),
=333×1000,
=333000;
(3)12
 -[12
-[12 -(3
-(3 +2.25-3.6)],
+2.25-3.6)],=12
 -12
-12 +(3
+(3 +2.25-3.6),
+2.25-3.6),=3.4+2.25-3.6,
=2.05;
(4)
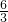 :6=
:6=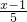 ,
,1:3=(x-1):5,
3×(x-1)=5,
3x-3=5,
3x-3+3=5+3,
3x=8,
3x÷3=8÷3,
x=
 ;
;(5)x-
 -
-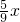 =
= ,
,x(1-
 )-
)- =
= ,
,x(1-
 )-
)- +
+ =
= +
+ ,
, x=
x= ,
, x×
x× =
= ×
× ,
,x=
 ;
;(6)a=8.8+8.98+8.998+8.9998+8.99998,
=(9-0.2)+(9-0.02)+(9-0.002)+(9-0.0002)+(9-0.00002),
=9×5-0.22222,
=45-0.22222,
=44.77778,
所以a的整数部分是44.
分析:(1)把3
 拆成3+
拆成3+ ,并把
,并把 化为小数,运用乘法分配律的逆运算简算;
化为小数,运用乘法分配律的逆运算简算;(2)观察可知,999是333的倍数,入江999×222转化为333×3×222,就可根据乘法分配律求出结果;
(3)根据数字特点,先去中括号,变为12
 -12
-12 +(3
+(3 +2.25-3.6),再把3
+2.25-3.6),再把3 化为小数,计算即可;
化为小数,计算即可;(4)先化简等式左边,原式变为1:3=(x-1):6,根据比例的基本性质改写成3×(x-1)=6,即3x-3=6,再根据等式的性质,两边同加上3,再同除以3即可;
(5)运用运算定律写成x(1-
 )-
)- =
= ,再根据等式的性质,两边同加
,再根据等式的性质,两边同加 ,得
,得 x=
x= ,两边再同乘
,两边再同乘 即可;
即可;(6)此算式中的数字很有特点,把每个数看作9减去小数的形式,通过计算即可得出.
点评:查了简便运算与解方程等题目,灵活运用所学的运算定律以及数与数之间的联系进行简便计算,在解方程时,注意依据等式的性质.

练习册系列答案
相关题目
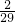 +
+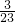 )×23×29
)×23×29 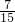 -
- -
- +
+
 +(2-1.4)÷
+(2-1.4)÷ ]÷
]÷
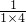 +
+ +
+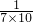 +…+
+…+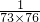 .
.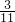 ÷(1
÷(1 ×1.48)×2.96÷2
×1.48)×2.96÷2 ×
×
 -(0.875×
-(0.875×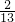 +1÷6.5÷8)×1
+1÷6.5÷8)×1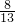 -
- ×18+
×18+ ×0.65.
×0.65.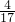 +5.2-
+5.2-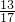
 +
+ +
+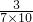 +…+
+…+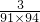
 +
+ )÷(
)÷(