题目内容
1.加工一批玩具,三天完成,第一天完成的是第二天的$\frac{2}{7}$,第三天完成的占这批玩具的$\frac{1}{3}$,己知第二天比第一天多做1000个,这批玩具共有多少个?分析 由题意知,把一批玩具的总数看作单位“1”,前两天完成的是总数的(1-$\frac{1}{3}$),则第一天完成的就是总数的(1-$\frac{1}{3}$)×$\frac{2}{2+7}$,第二天完成的是总数的(1-$\frac{1}{3}$)×$\frac{7}{2+7}$,已知第二天比第一天多做1000个,也就是多做了总数的[(1-$\frac{1}{3}$)×$\frac{7}{2+7}$-(1-$\frac{1}{3}$)×$\frac{2}{2+7}$],要求这批玩具共有多少个,就是求单位“1”的量是多少,根据分数除法的意义,列式解答即可.
解答 解:1000÷[(1-$\frac{1}{3}$)×$\frac{7}{2+7}$-(1-$\frac{1}{3}$)×$\frac{2}{2+7}$]
=1000÷[$\frac{14}{27}$-$\frac{4}{27}$]
=1000×$\frac{27}{10}$
=2700(个)
答:这批玩具共有2700个.
点评 解答本题的关键是,把两个不同的单位“1”转化成同一单位“1”,再利用“对应数÷对应分率=单位“1”的量”解答.

练习册系列答案
相关题目
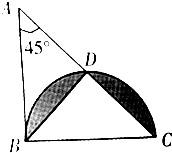 如图中,直角三角形ABC的面积是12平方厘米.聪明的你,请算一算阴影部分的面积是多少平方厘米.
如图中,直角三角形ABC的面积是12平方厘米.聪明的你,请算一算阴影部分的面积是多少平方厘米.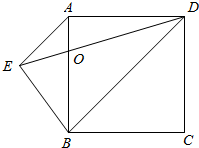 如图所示,ABCD是边长为12厘米的正方形,梯形AEBD的对角线相交于O,三角形AOE的面积比三角形BOD的面积小26平方厘米,梯形AEBD的面积是多少平方厘米?
如图所示,ABCD是边长为12厘米的正方形,梯形AEBD的对角线相交于O,三角形AOE的面积比三角形BOD的面积小26平方厘米,梯形AEBD的面积是多少平方厘米?