题目内容
如图：四边形ABCD的面积是520平方厘米，四边形ABED是正方形，DE与EC的长度比为5：3，三角形DEC的面积是多少平方厘米？
解：设ED=5a，EC=3a，
则（5a+5a+3a）×5a÷2=520，
13a×5a÷2=520，
65a2=520×2=1040，
所以a2=16
三角形DEC的面积为：3a×5a÷2=15a2÷2=15×16÷2=120（平方厘米）；
答：三角形DEC的面积是120平方厘米．
分析：由“DE与EC的长度比为5：3，”设ED=5a，EC=3a，则根据梯形的面积公式S=（a+b）h÷2，得出四边形ABCD的面积为：（5a+5a+3a）×5a÷2=520，由此求出a2的值，再根据三角形的面积公式S=ah÷2，求出三角形DEC的面积．
点评：本题主要是灵活利用梯形的面积公式、三角形的面积公式与代换的方法解决问题．
则（5a+5a+3a）×5a÷2=520，
13a×5a÷2=520，
65a2=520×2=1040，
所以a2=16
三角形DEC的面积为：3a×5a÷2=15a2÷2=15×16÷2=120（平方厘米）；
答：三角形DEC的面积是120平方厘米．
分析：由“DE与EC的长度比为5：3，”设ED=5a，EC=3a，则根据梯形的面积公式S=（a+b）h÷2，得出四边形ABCD的面积为：（5a+5a+3a）×5a÷2=520，由此求出a2的值，再根据三角形的面积公式S=ah÷2，求出三角形DEC的面积．
点评：本题主要是灵活利用梯形的面积公式、三角形的面积公式与代换的方法解决问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图平行四边形ABCD的面积是36平方厘米，其中AE=
如图，四边形ABCD内有一点O，且O点到四条边AB、BC、CD、AD的距离都等于8厘米．若四边形ABCD的周长是62厘米．那么，四边形ABCD的面积是
如图，四边形ABCD的周长是60厘米，点M到各边的距离都是4.5厘米，这个四边形的面积是
如图，四边形ABCD是边长为8厘米的正方形，三角形ADF的面积比三角形CEF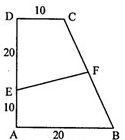
如图，四边形ABCD是直角梯形，∠A=∠D=90?，点E将DA分成2：1，F为BC中点，则四边形FEAB的面积为