题目内容
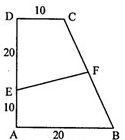 如图,四边形ABCD是直角梯形,∠A=∠D=90?,点E将DA分成2:1,F为BC中点,则四边形FEAB的面积为
如图,四边形ABCD是直角梯形,∠A=∠D=90?,点E将DA分成2:1,F为BC中点,则四边形FEAB的面积为分析:观察图形可知,连接AE、BE,则四边形EFAB被分成两部分,不难看出,三角形AEB和三角形DEC等底等高,所以面积相等,又因为F是BC的中点,所以三角形CEF和三角形BEF的面积相等,那么四边形FEAB和四边形EFCD的面积相等都等于这个梯形的面积的一半,据此利用梯形的面积公式求出梯形的面积,再除以2即可.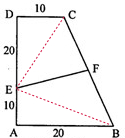

解答:解:连接AE、BE,

则四边形EFAB被分成两部分,三角形AEB和三角形DEC等底等高,所以面积相等,
又因为F是BC的中点,所以三角形CEF和三角形BEF的面积相等,
那么四边形FEAB和四边形EFCD的面积相等都等于这个梯形的面积的一半,是:
(10+20)×(10+20)÷2÷2
=30×30÷2÷2
=45÷2
=22.5
答:四边形FEAB的面积为 22.5.
故答案为:22.5.

则四边形EFAB被分成两部分,三角形AEB和三角形DEC等底等高,所以面积相等,
又因为F是BC的中点,所以三角形CEF和三角形BEF的面积相等,
那么四边形FEAB和四边形EFCD的面积相等都等于这个梯形的面积的一半,是:
(10+20)×(10+20)÷2÷2
=30×30÷2÷2
=45÷2
=22.5
答:四边形FEAB的面积为 22.5.
故答案为:22.5.
点评:此题主要考查等底等高的三角形的面积相等的性质的应用,关键是正确画出辅助线.

练习册系列答案
相关题目
 如图平行四边形ABCD的面积是36平方厘米,其中AE=
如图平行四边形ABCD的面积是36平方厘米,其中AE= 如图,四边形ABCD内有一点O,且O点到四条边AB、BC、CD、AD的距离都等于8厘米.若四边形ABCD的周长是62厘米.那么,四边形ABCD的面积是
如图,四边形ABCD内有一点O,且O点到四条边AB、BC、CD、AD的距离都等于8厘米.若四边形ABCD的周长是62厘米.那么,四边形ABCD的面积是 如图,四边形ABCD的周长是60厘米,点M到各边的距离都是4.5厘米,这个四边形的面积是
如图,四边形ABCD的周长是60厘米,点M到各边的距离都是4.5厘米,这个四边形的面积是 如图,四边形ABCD是边长为8厘米的正方形,三角形ADF的面积比三角形CEF
如图,四边形ABCD是边长为8厘米的正方形,三角形ADF的面积比三角形CEF