题目内容
 如图平行四边形ABCD的面积是36平方厘米,其中AE=
如图平行四边形ABCD的面积是36平方厘米,其中AE=| 2 | 3 |
分析:由题意“平行四边形ABCD中AE=
AC”,可得出AE=2EC,又由△ABE与△BEC的高相等,得出△ABE的面积是△BEC的面积的2倍,△ABE的面积是△ABC面积的
,又由“平行四边形的面积是36平方厘米”,△ABC面积是平行四边形的面积的
,进行等量代换,从而算出阴影部分的面积.
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
解答:解:因为AE=
AC,AE+EC=AC,
所以CE=
AE,
又因为△ABE与△EBC等高,
所以S△ABE=2S△EBC,
所以S△ABE=
S△ABC,
又因为S平行四边形ABCD=36(平方厘米),
所以S△ABC=
S平行四边形ABCD=
×36=18(平方厘米),
所以S△ABE=
×18=12(平方厘米);
答:阴影部分的面积是12平方厘米.
| 2 |
| 3 |
所以CE=
| 1 |
| 2 |
又因为△ABE与△EBC等高,
所以S△ABE=2S△EBC,
所以S△ABE=
| 2 |
| 3 |
又因为S平行四边形ABCD=36(平方厘米),
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
所以S△ABE=
| 2 |
| 3 |
答:阴影部分的面积是12平方厘米.
点评:此题主要是根据条件先求三角形ABC的面积,再找△ABE的面积与三角形ABC的面积之间的关系,求出阴影部分的面积.

练习册系列答案
相关题目
 (2012?中山市模拟)如图,三角形ABC是面积为46.8平方厘米的等边三角形,ABCD是平行四边形,圆的半径是6厘米,求阴影部分的面积.
(2012?中山市模拟)如图,三角形ABC是面积为46.8平方厘米的等边三角形,ABCD是平行四边形,圆的半径是6厘米,求阴影部分的面积. (2011?苏州模拟)求图中阴影部分的面积.
(2011?苏州模拟)求图中阴影部分的面积.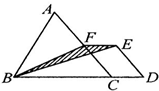 如图,三角形ABC的面积是50cm2,是平行四边形EFCD面积的2倍,图中阴影部分的面积是
如图,三角形ABC的面积是50cm2,是平行四边形EFCD面积的2倍,图中阴影部分的面积是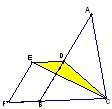 如图,三角形ABC的面积是24平方厘米,是平行四边形BDEF面积的2倍,则涂色部分的面积是
如图,三角形ABC的面积是24平方厘米,是平行四边形BDEF面积的2倍,则涂色部分的面积是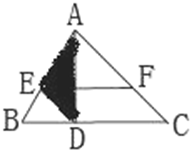 如图,三角形ABC的面积是60平方厘米,平行四边形DCFE是面积是三角形ABC的
如图,三角形ABC的面积是60平方厘米,平行四边形DCFE是面积是三角形ABC的