题目内容
如图，第一个图是一个水平摆放的小正方体，第二、第三个图是由同样的小正方体木块叠放而成，按照这样的规律继续叠放至第七层时，小正方体木块总数应是（ ）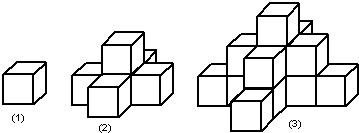
分析：图（1）中只有一层，有（4×0+1）一个正方形，图（2）中有两层，在图（1）的基础上增加了一层，第二层有（4×1+1）个．图（3）中有三层，在图（2）的基础上增加了一层，第三层有（4×2+1），依此类推当图形有七层时总的正方体的个数．
解答：解：当图形有七层时，最下面一层的个数为：（4×6+1），
则此时总的正方体个数为：
1+（4×1+1）+（4×2+1）+（4×3+1）+（4×4+1）+（4×5+1）+（4×6+1）=91．
故答案为：91．
则此时总的正方体个数为：
1+（4×1+1）+（4×2+1）+（4×3+1）+（4×4+1）+（4×5+1）+（4×6+1）=91．
故答案为：91．
点评：本题考查了规律型：图形的变化．解题关键是根据图形的变换总结规律，由图形变换得规律：每次都比上一次增加一层，增加第n层时小正方形共增加了4（n-1）+1个，将n层的小正方形个数相加即可得到总的小正方形个数．
练习册系列答案
相关题目
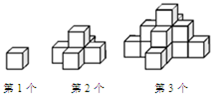如图，第一个图形是一个水平摆放的小正方体木块，第二个图形和第三个图形是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，若某个叠放的图形中，小正方体木块总数为153个，则这个图形是第
老师吩咐生活委员安排一个小组的同学明天下午去帮助一年级同学种树，四个小组的同学都争着去．请你利用如图的圆设计一个转盘来决定哪个小组去．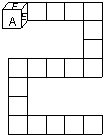
如图第一格内放着一个立方体，六个面上分别写着A、B、C、D、E、F，其中A与D、B与E、C与F相对．如果将立方体沿着图中的方格滚动，滚动了16次后，向上的一面写的字母是
一个农民牵着一头牛从甲地到乙地去放牧，从甲地到乙地有两条路，第一条路是一个大半圆，第二条路是两个不同小半圆（如图1）．