题目内容
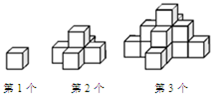 如图,第一个图形是一个水平摆放的小正方体木块,第二个图形和第三个图形是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,若某个叠放的图形中,小正方体木块总数为153个,则这个图形是第
如图,第一个图形是一个水平摆放的小正方体木块,第二个图形和第三个图形是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,若某个叠放的图形中,小正方体木块总数为153个,则这个图形是第9
9
个图形.分析:图(1)中只有一层,有(4×0+1)一个正方形,图(2)中有两层,在图(1)的基础上增加了一层,第二层有(4×1+1)个.图(3)中有三层,在图(2)的基础长增加了一层,第三层有(4×2+1),依次类推当图形有二层和七层时总的正方形的个数.
解答:解:根据分析:当图形有二层时,第二层的正方形个数为:(4×1+1),则此时总的正方形个数为1+(4×1+1)=6;
当图形有七层时,第七层的个数为:(4×6+1),则此时总的正方形个数为:1+(4×1+1)+(4×2+1)+(4×3+1)+(4×4+1)+(4×5+1)+(4×6+1)=91.
当图形有8层时,第八层的个数为:(4×7+1),则此时总个数是:1+(4×1+1)+(4×2+1)+(4×3+1)+(4×4+1)+(4×5+1)+(4×6+1)+(4×7+1)=120,
当图形有9层是,第九层的个数是:(4×8+1),则此时总个数是:1+(4×1+1)+(4×2+1)+(4×3+1)+(4×4+1)+(4×5+1)+(4×6+1)+(4×7+1)+(4×8+1)=153,
答:当正方体的总块数是153时,这个图形有9层,是第9个图形.
故答案为:9.
当图形有七层时,第七层的个数为:(4×6+1),则此时总的正方形个数为:1+(4×1+1)+(4×2+1)+(4×3+1)+(4×4+1)+(4×5+1)+(4×6+1)=91.
当图形有8层时,第八层的个数为:(4×7+1),则此时总个数是:1+(4×1+1)+(4×2+1)+(4×3+1)+(4×4+1)+(4×5+1)+(4×6+1)+(4×7+1)=120,
当图形有9层是,第九层的个数是:(4×8+1),则此时总个数是:1+(4×1+1)+(4×2+1)+(4×3+1)+(4×4+1)+(4×5+1)+(4×6+1)+(4×7+1)+(4×8+1)=153,
答:当正方体的总块数是153时,这个图形有9层,是第9个图形.
故答案为:9.
点评:本题考查了图形的变化规律,解题关键是根据图形的变换总结规律:每次都比上一次增加一层,增加第n层时小正方形增加了4(n-1)+1个,将n层的小正方形个数相加即可得到总的小正方形个数.

练习册系列答案
相关题目
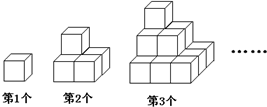 如图,第1个图形是一个水平摆放的小正方体木块,第2个图形和第3个图形是由这样的小正方体叠放而成的.按照这样的规律继续叠放下去,第7个图形中,从正面看,看得到的木块应有
如图,第1个图形是一个水平摆放的小正方体木块,第2个图形和第3个图形是由这样的小正方体叠放而成的.按照这样的规律继续叠放下去,第7个图形中,从正面看,看得到的木块应有