题目内容
 如图,已知AB=AC,∠1=
如图,已知AB=AC,∠1=110°
110°
,∠2=35°
35°
,∠3=35°
35°
.分析:观察图形可知,∠1与70°的角正好组成一个平角,所以可以求出∠1=180°-70°=110°;又因为AB=AC,所以三角形ABC是等腰三角形,则∠2=∠3,根据三角形内角和定理即可求出∠2和∠3的度数.
解答:解:∠1=180°-70°=110°;
又因为AB=AC,所以三角形ABC是等腰三角形,
则∠2=∠3=(180°-110°)÷2=35°,
故答案为:110°;35°;35°.
又因为AB=AC,所以三角形ABC是等腰三角形,
则∠2=∠3=(180°-110°)÷2=35°,
故答案为:110°;35°;35°.
点评:此题主要考查平角的意义、等腰三角形的性质以及三角形内角和定理的综合应用.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图,已知等腰三角形ABC,D为AC中点,AB=BC=2厘米,
如图,已知等腰三角形ABC,D为AC中点,AB=BC=2厘米,
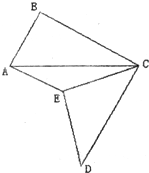 如图,已知AB=AE=4cm,BC=DC,∠BAE=∠BCD=90°,AC=10cm,则S△ABC+S△ACE+S△CDE
如图,已知AB=AE=4cm,BC=DC,∠BAE=∠BCD=90°,AC=10cm,则S△ABC+S△ACE+S△CDE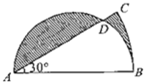 如图,已知AB=AC=12厘米,并且小阴影部分的面积为3.26厘米2,求大阴影部分的面积.
如图,已知AB=AC=12厘米,并且小阴影部分的面积为3.26厘米2,求大阴影部分的面积.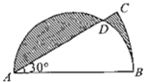 如图,已知AB=AC=12厘米,并且小阴影部分的面积为3.26厘米2,求大阴影部分的面积.
如图,已知AB=AC=12厘米,并且小阴影部分的面积为3.26厘米2,求大阴影部分的面积.