题目内容
 如图,已知等腰三角形ABC,D为AC中点,AB=BC=2厘米,
如图,已知等腰三角形ABC,D为AC中点,AB=BC=2厘米, |
| DE |
 |
| DF |
分析:如图所示,连接BD,三角形ABC、三角形BDC和三角形DBA都是等腰直角三角形,且AD=DC=BD,所以扇形BDE与扇形ADF的面积相等,于是可将扇形BDE平移到扇形ADF的位置,则阴影部分的面积等于三角形ABC面积的一半,又因三角形的AB=BC=2厘米,所以可以求出阴影部分的面积.
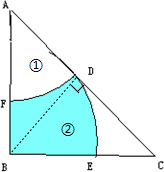

解答:解:如图所示,将扇形②平移到扇形①的位置,
阴影部分的面积=
三角形ABC的面积;
即:阴影部分的面积:
2×2÷2÷2
=4÷2÷2,
=2÷2,
=1(平方厘米);
答:阴影部分的面积是1平方厘米.
阴影部分的面积=
| 1 |
| 2 |
即:阴影部分的面积:
2×2÷2÷2
=4÷2÷2,
=2÷2,
=1(平方厘米);
答:阴影部分的面积是1平方厘米.
点评:解答此题的关键是作出辅助线,求得:阴影部分的面积等于三角形ABC面积的一半.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
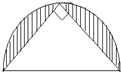 (2013?蓬溪县模拟)如图,已知等腰三角形的面积是50平方厘米,阴影部分的面积是
(2013?蓬溪县模拟)如图,已知等腰三角形的面积是50平方厘米,阴影部分的面积是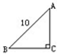 如图,已知等腰直角三角形的斜边AB长10厘米,求这个三角形的面积.
如图,已知等腰直角三角形的斜边AB长10厘米,求这个三角形的面积.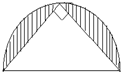 如图,已知等腰三角形的面积是50平方厘米,阴影部分的面积是________平方厘米.
如图,已知等腰三角形的面积是50平方厘米,阴影部分的面积是________平方厘米.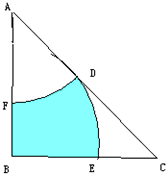 如图,已知等腰三角形ABC,D为AC中点,AB=BC=2厘米,
如图,已知等腰三角形ABC,D为AC中点,AB=BC=2厘米, ,
, 分别是以B、A为圆心的弧.那么阴影部分的面积是多少平方厘米?
分别是以B、A为圆心的弧.那么阴影部分的面积是多少平方厘米?