题目内容
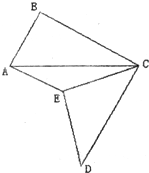 如图,已知AB=AE=4cm,BC=DC,∠BAE=∠BCD=90°,AC=10cm,则S△ABC+S△ACE+S△CDE
如图,已知AB=AE=4cm,BC=DC,∠BAE=∠BCD=90°,AC=10cm,则S△ABC+S△ACE+S△CDE50
50
cm2(注:S△ABC表示三角形ABC的面积)
分析:此题需将将三角形ABC绕A点和C点分别顺时针和逆时针旋转90°,构成三角形AEC′和A′DE,再连接A′C′,
显然AC⊥AC′,AC⊥A′C,AC=A′C=AC′,
所以,ACA′C是正方形,三角形AEC′和三角形A′DC关于正方形的中心O点中心对称,
在中心对称图形ACA′C中有如下等量关系:S△AEC=S△A′DC;S△AEC′=S△A′DC;SACED=SAC′DE;
所以S△ABC+A△ACE+S△CDE=S△AEC′+S△C′DE+S△A′C′D=
SACA′C′=
×10×10=50cm2
从而问题得解.
显然AC⊥AC′,AC⊥A′C,AC=A′C=AC′,
所以,ACA′C是正方形,三角形AEC′和三角形A′DC关于正方形的中心O点中心对称,
在中心对称图形ACA′C中有如下等量关系:S△AEC=S△A′DC;S△AEC′=S△A′DC;SACED=SAC′DE;
所以S△ABC+A△ACE+S△CDE=S△AEC′+S△C′DE+S△A′C′D=
| 1 |
| 2 |
| 1 |
| 2 |
从而问题得解.
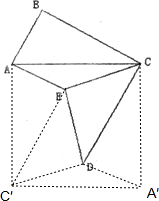
解答:解:将三角形ABC绕A点和C点分别顺时针和逆时针旋转90°,构成三角形AEC′和A′DE,再连接A′C′,显然AC⊥AC′,AC⊥A′C,AC=A′C=AC′,
所以,ACA′C是正方形,三角形AEC′和三角形A′DC关于正方形的中心O点中心对称,
在中心对称图形ACA′C中有如下等量关系:S△AEC=S△A′DC;S△AEC′=S△A′DC;SACED=SAC′DE;
所以S△ABC+A△ACE+S△CDE=S△AEC′+S△C′DE+S△A′C′D=
SACA′C′=
×10×10=50cm2
答:S△ABC+S△ACE+S△CDE是50平方厘米.
故答案为:50.
所以,ACA′C是正方形,三角形AEC′和三角形A′DC关于正方形的中心O点中心对称,
在中心对称图形ACA′C中有如下等量关系:S△AEC=S△A′DC;S△AEC′=S△A′DC;SACED=SAC′DE;
所以S△ABC+A△ACE+S△CDE=S△AEC′+S△C′DE+S△A′C′D=
| 1 |
| 2 |
| 1 |
| 2 |

答:S△ABC+S△ACE+S△CDE是50平方厘米.
故答案为:50.
点评:解决此题的关键是将三角形ABC绕A点和C点分别顺时针和逆时针旋转90°,形成一个中心对称图形,即正方形,从而得到所求图形的面积与正方形面积的关系,问题得解.

练习册系列答案
相关题目
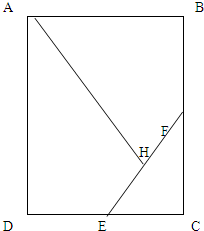 如图,在长方形ABCD中,已知E是DC的中点,F是BC的中点,H是FE的中点,AB=12分米,BC=20分米,那么三角形AHE的面积是多少?(提示:连接AE、AF)
如图,在长方形ABCD中,已知E是DC的中点,F是BC的中点,H是FE的中点,AB=12分米,BC=20分米,那么三角形AHE的面积是多少?(提示:连接AE、AF)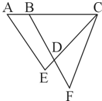 如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的
如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的
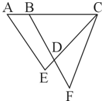 如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的________倍.
如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的________倍.