题目内容
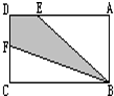 如图长方形ABCD中,AD=4DE,F为CD的中点,AB=4cm,BC=5cm.阴影部分的面积是
如图长方形ABCD中,AD=4DE,F为CD的中点,AB=4cm,BC=5cm.阴影部分的面积是7.5
7.5
cm2.分析:阴影部分的面积=长方形ABCD的面积-△ABE的面积-△BCF的面积.长方形ABCD的面积=长×宽,长、宽均已知,即可求出;在△ABE中,∠A=90°,AB=4cm,因为AD=4DE,所以AE=5×
=
(cm),根据三角形的面积公式S=
ah即可求出;在△BCF中,∠C=90°,BC=5cm,因为F为CD的中点,所以CF=
=
=2(cm),根据三角形的面积公式S=
ah即可求出.
| 3 |
| 4 |
| 15 |
| 4 |
| 1 |
| 2 |
| CD |
| 2 |
| 4 |
| 2 |
| 1 |
| 2 |
解答:解:如图,

5×4-
×4×
-
×5×
=20-7.5-5
=7.5(cm2);
故答案为:7.5

5×4-
| 1 |
| 2 |
| 15 |
| 4 |
| 1 |
| 2 |
| 4 |
| 2 |
=20-7.5-5
=7.5(cm2);
故答案为:7.5
点评:本题是考查求组合图形的面积,此题很容易看出阴影部分的面积=长方形ABCD的面积-△ABE的面积-△BCF的面积,关键是在△ABE中求出AE,在△BCF中求出CF.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图长方形ABCD中,E在AD上,AE的长是AD的
如图长方形ABCD中,E在AD上,AE的长是AD的 如图长方形ABCD中,AB:BC=5:4,位于A点的第一只蚂蚁按A→B→C→D→A方向爬行,位于C点的第二只蚂蚁按C→B→A→D→C的方向同时出发,分别沿长方形的边爬行,如果两只蚂蚁第一次在B点相遇,则两只蚂蚁第二次相遇在( )边上.
如图长方形ABCD中,AB:BC=5:4,位于A点的第一只蚂蚁按A→B→C→D→A方向爬行,位于C点的第二只蚂蚁按C→B→A→D→C的方向同时出发,分别沿长方形的边爬行,如果两只蚂蚁第一次在B点相遇,则两只蚂蚁第二次相遇在( )边上. 如图长方形ABCD中,AD=4DE,F为CD的中点,AB=4cm,BC=5cm.阴影部分的面积是________cm2.
如图长方形ABCD中,AD=4DE,F为CD的中点,AB=4cm,BC=5cm.阴影部分的面积是________cm2. 如图长方形ABCD中,E在AD上,AE的长是AD的
如图长方形ABCD中,E在AD上,AE的长是AD的 ,F在DC上,DF的长是DC的
,F在DC上,DF的长是DC的 ,三角形BEF的面积是378cm2,长方形ABCD的面积是多少?
,三角形BEF的面积是378cm2,长方形ABCD的面积是多少?