题目内容
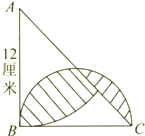 如图,△ABC是等腰直角三角形,求图中阴影部分的面积.
如图,△ABC是等腰直角三角形,求图中阴影部分的面积.分析:要求阴影部分的面积,可用半圆面积减去里面的空白面积,求空白面积可用三角形面积减去扇形面积.
解答: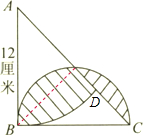 解:设等腰直角三角形ABC的直角边为r,
解:设等腰直角三角形ABC的直角边为r,
r2=72,r2=144;
45°÷360°=
;
扇形ABD的面积:
×3.14×144=3.14×18=56.52(平方厘米),
空白面积BCD的面积:
72÷2-(56.52-72÷2),
=36-(56.52-36),
=36-20.52,
=15.48(平方厘米),
半圆面积:
×3.14×144×
,
=3.14×18,
=56.52(平方厘米),
阴影面积:56.52-15.48=41.04(平方厘米).
答:阴影部分面积是41.04平方厘米.
 解:设等腰直角三角形ABC的直角边为r,
解:设等腰直角三角形ABC的直角边为r,| 1 |
| 2 |
45°÷360°=
| 1 |
| 8 |
扇形ABD的面积:
| 1 |
| 8 |
空白面积BCD的面积:
72÷2-(56.52-72÷2),
=36-(56.52-36),
=36-20.52,
=15.48(平方厘米),
半圆面积:
| 1 |
| 2 |
| 1 |
| 4 |
=3.14×18,
=56.52(平方厘米),
阴影面积:56.52-15.48=41.04(平方厘米).
答:阴影部分面积是41.04平方厘米.
点评:此题主要考查求阴影部分的面积,可以按一般思路去解答,就是用半圆面积减去里面的空白面积,而空白面积可用三角形面积减去扇形面积.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 如图,△ABC是等腰直角三角形,以直角边AB为直径作半圆,与斜边AC交于D,且AB=20厘米,求阴影部分的面积.
如图,△ABC是等腰直角三角形,以直角边AB为直径作半圆,与斜边AC交于D,且AB=20厘米,求阴影部分的面积. 如图,△ABC是等腰直角三角形,已知AE=4cm,长方形DGFE的长DG是它的宽DE的3倍.则△ABC的面积是
如图,△ABC是等腰直角三角形,已知AE=4cm,长方形DGFE的长DG是它的宽DE的3倍.则△ABC的面积是 如图,ABC是等腰直角三角形,D是半圆周的中点,BC是半圆的直径.已知AB=BC=10厘米,那么阴影部分的面积是
如图,ABC是等腰直角三角形,D是半圆周的中点,BC是半圆的直径.已知AB=BC=10厘米,那么阴影部分的面积是 如图,ABC是等腰直角三角形,它的内部有两个小正方形,求阴影部分的面积.
如图,ABC是等腰直角三角形,它的内部有两个小正方形,求阴影部分的面积.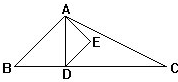 如图三角形ABC是等腰三角形.AB=AC,BAC=120°.三角形ADE是正三角形,点D在BC边上,BD:DC=2:3.当三角形ABC的面积是50cm2时,三角形ADE的面积是多少?
如图三角形ABC是等腰三角形.AB=AC,BAC=120°.三角形ADE是正三角形,点D在BC边上,BD:DC=2:3.当三角形ABC的面积是50cm2时,三角形ADE的面积是多少?